مثال عدد پی؛ فیزیکی نبودن و ذهنی نبودن عدد پی
جلسه قبل مسامحتاً تعبیری شد؛ جلوتر بحث کرده بودیم ولی توضیح آن را در مثالی که زدم عرض میکنم؛ عرض کردم کمّیّتها با هم نسبت برقرار میکنند. شرط برقرار شدن نسبت بین دو کمیت، این است که دو کمیت متجانس باشند. یعنی خط با خط، نسبت برقرار میکنند. اما خط با سطح نسبتی برقرار نمیکند؛ چون دو جنس هستند؛ جنس بهمعنای هندسی. سطح با حجم نسبتی برقرار نمیکند، چون دو تا هستند. اما سطح با سطح و همچنین حجم با حجم، نسبت برقرار میکنند. پس شرط برقراری نسبت بین کمیتها، تجانس دو کمیت است؛ باید همجنس باشند و متخالف نباشند. آن چه که بسیار مهم بود و مرحوم خواجه هم در مقاله عاشره اصول اقلیدس دارند، این است: وقتی دو کمیت، نامتجانس بودند و متخالف بودند نسبت برقرار نمیکنند. البته میتوانید ثالثی را واسطه قرار بدهید و نسبت برقرار کنید. آنها در مباحثه اصول اقلیدس بحث شده است. یعنی خط را به کم منفصل ببرید و سطح را هم به کم منفصل ببرید، وقتی دو عدد، هم جنس شدند، بین آنها نسبت برقرار میکنید؛ این مشکلی ندارد. علی ای حال مادامی که متخالف هستند، نسبتی برقرار نمیشود. اما وقتی متجانس شدند، نسبت برقرار میشود، اما بین دو کمیت متجانس که بین آنها نسبت برقرار میشود، دو جور کمیت داریم: کمیتهای متشارک و کمیتهای متباین. در جلسه قبل عرض کردم تجانس و تباین، [که درست نیست،] بلکه تشارک و تباین است. واژه تشارک را در آنجا تصحیح کنید؛ متشارک و متباین.
متشارک و متباین چه هستند؟ هفته قبل توضیح دادم. مثلاً دو خط با هم نسبت دارند، چون متجانس هستند. اما لازم نکرده دو خط، دائماً متشارک باشند، و حال اینکه بر عالم ریاضیات سالها گذشت و هنوز جذر عدد دو و عدد گنگ کشف نشده بود، باورشان این بود که هر دو مقدار متجانس، متشارک هم هستند؛ یعنی خلاصه به یک جزء کوچکی میرسید که میتواند عادّ هر دو باشد. متشارک، یعنی دو کمیت تشارک دارند در اینکه یک عاد مشترک دارند؛ یک جزء کوچکی هر دو را به عدد صحیح میشمارد. بعد به مسأله ضلع و قطر رسیدیم. طبق قانون فیثاغورس وقتی میخواستند بگویند جذر [مجموع مربعات] دو ضلع مساوی با جذر مربع وتر است، لذا [برای مربعی با ضلع واحد به منظور محاسبه قطر،] خواستند جذر دو را بگیرند؛ تاریخش معروف است و یکی از معروفترین مطالب ریاضیات است؛ قبل از دو هزار سال پیش است. بعد به این رسیدند که قطر مربع بهعنوان یک خط، با ضلع بهعنوان یک خط که هر دو هم خط مستقیم است، متشارک نیستند؛ یعنی محال است شما به یک پارهخط بسیار ریزی برسید که هر دو را بشمارد. به این، رادیکال دو میگوییم. جذر دو و قطر مربع، گنگ است. خیلی مطلب مهمی است. اولین بحران در ریاضیات بود. پس این نظرتان باشد: کمیتهای متجانس نسبت برقرار میکنند اما کمیتهای متجانس دو جور داریم؛ کمیتهای متجانس متشارک که عاد واحد دارند، کمیتهای متجانس متباین که گنگ هستند و اصم هستند.
آیا خط مستقیم با خط منحنی، دو جنس هستند یا یک جنس هستند؟ خلاصه طول هستند. در اینجا روی یک نگاهی که همه دارند و پذیرفته شده است، خط منحنی با خط مستقیم از حیث کمیت طول، متجانس هستند. ولذا در دایره، محیط آن منحنی است اما قطرش خط مستقیم است؛ میگویید نسبت محیط دایره به قطر، سه و چهارده صدم است. یعنی میتوانید قطر را سه بار روی محیط دایره بغلطانید که مقداری هم زیاد میآید؛ سه و چهارده صدم؛ محیط سه برابر و خوردهای از قطر خودش است. قطر، ضرب در سه و چهارده صدم، نزدیک به محیط دایره میشود. خُب این نسبتی شد بین دو کمیت متجانس؛ نسبت محیط بر قطر. این چه نسبتی است؟ متباین است یا متشارک است؟ این خیلی طول کشید. خُب قطر مربع [با ضلع مربع] دو هزار و پانصد سال پیش معلوم بود که متباین هستند. اما اینکه آیا قطر با محیط، متباین هستند یا نه، تا حدود دویست سال پیش در تاریخ طول کشیده تا بشر مطمئن شود و برهان بیاورد که نسبت محیط با قطر، نسبتی است که تا بینهایت میرود و اصم است؛ به یک عاد مشترک واحد نمیرسند.
حالا من هفته قبل چرا این مثال را عرض کردم؟ عکسی هم در آن جا گذاشتند. این عکس[1] را نگاه کنید. چیزی که کار طلبگی ما است، نشاندادن یک مطلبی است که همه بشر، امروزه هر کجا بروید قبول میکنند. یعنی یک جایی نمیروید بگویند فلانی قبول ندارد، مگر [اینکه] درسش را نخوانده باشد. آن مانعی ندارد، خیلی از افراد هستند که فنی را نمیدانند و چیزی را قبول ندارند. و الا کسانی که درسش را خواندهاند و مطلب را میدانند، بین متخصصین آن رشته، محل اختلاف نیست؛ عرض کردم الآن برای آنها ثابت است.
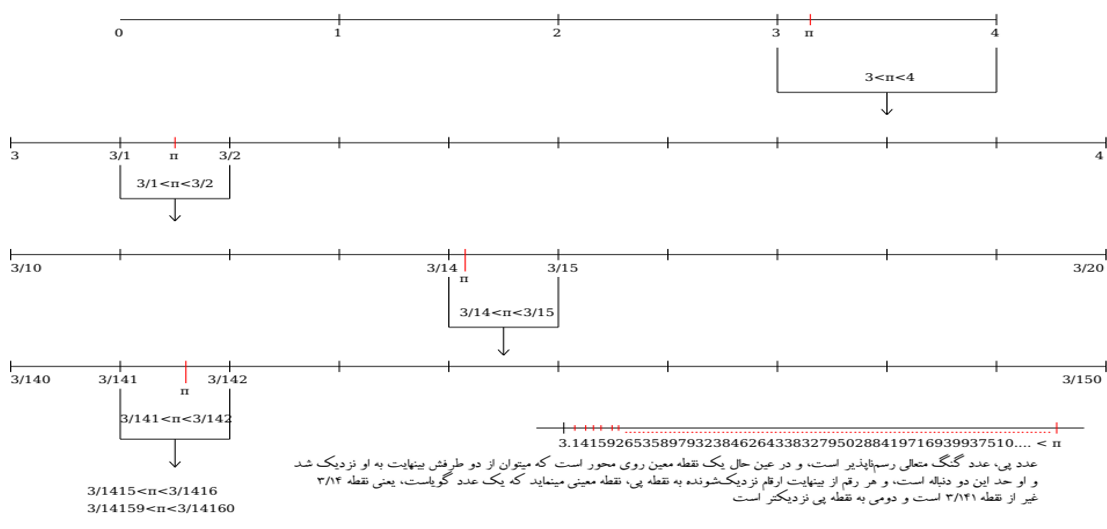
عدد پی همان عدد دایره است. کلمه «Periphery» در یونانی بهمعنای [محیط] دایره است. عدد پی، یعنی عدد [محیط] دایره. گنگ بودن آن به چه معنا است؟ روی این عکس تأمل خوبی کنید. اول مقصود از این تصویر را تصور کنید و بعد برای دیگران هم میتوانید بهخوبی واضح کنید. حاصلش این است: مثلاً شما میگویید اعداد اول بینهایت هستند. چقدر ریاضیدانها از بینهایتها بحث کردهاند. جلسه قبل بود [که] عرض کردم هیلبرت گفت: «بیخودی زحمت نکش، آن فردوس و بهشتی که کانتور برای ما خلق کرد، احدی نمیتواند در آن خدشه کند». خُب آنها برای خودش یک چیزهایی بود. آنها دیده بودند.
اما آنچه که این عکس آن را میرساند، این است: در یک خط روشن جلوی چشم هر کسی است؛ اگر مطلب را که مشترک بین کل بشر است تصور کند، با یک مطلب مشترک بین الکل مواجه میشود؛ که آن چیست؟ بینهایت رقم معین است. کجا؟ روی خطی که جلوی چشم همه ما است. یعنی یک پارهخط جلوی چشم ما است، میگوید این را نگاه کن، بینهایت رقمی که معین است دارد؛ اگر پنجِ آن را، شش کنید، خراب میشود. این بینهایت، هست؟ بله. معین است یا نه؟ بله، حتماً معین است. خُب این بینهایت رقمی که هست، بشر آن را خلق میکند؟ آن را فرض میگیرد؟ نه، آن را کشف میکند.
کتاب «The mathematical experience»؛ «تجربه ریاضیاتی» برای دو نفر بود که جلسه قبل عرض کردم. او چه گفته بود؟ مطلب بسیار مهمی گفته بود. گفت اکثر ریاضیدانها –من که عرض میکنم تمام آنها، در این تردیدی ندارم؛ حالِ طلبگی است- وقتی فکر میکنند و ریاضیات را پیش میبرند، تمامش افلاطونی است. یعنی اصلاً ذهن او و کارکرد او و درک او بهصورت ناخودآگاه، همه، اینها است. بعد گفت وقتی سر به سر آنها بگذارید و بگویید حالا بگو ببینم –«بگو ببینم» تعبیر قشنگی بود-، از افلاطونگرائی که ناخودآگاه اعمال میکرد، بهسوی فرمالیسم عقبنشینی میکند. یعنی مدام میخواهد که یک جوری اینها را توجیه کند. چرا مجبور است که توجیه کند؟ عرض من این بود: چون الآن زمینهی درستِ توجیهِ افلاطونگرائی در دست ما موجود نیست. اگر کسانی این مطالب را درک کنند و سپس به نحو واضح، آن امر ارتکازی را به صحنه بیاورند و با مثالها و … آن را مدون کنند، دیگر آن ریاضیدان مجبور نیست که وقتی سر به سرش میگذارید، عقبنشینی کند. ابزار قوی توجیهِ همان چیزی که انجام میدهد را به شما عرضه میکند. همه مطلوب من، این است. اگر هم وقت شما را گرفتم برای این است. این کار، خیلی ارزشمند است که شما بحث را طوری جلو ببرید و آن را آغشته به بحثهای فلسفی و متافیزیکی نکنید، صرفاً ریاضیاتی باشد و روی همان مفهوم ساذج، به ذهن همه نشان بدهید که این اعداد، متعین هستند. اگر ما هم نبودیم این عدد، متعین است. ما داریم آن را کشف میکنیم. بعد از اینکه کشفش کردیم، سؤال کنیم وقتی عدد پی کشف شد، کدام رقمِ پنجاهمین آن، جزء عدد پی و رقم پی است؟ مثلاً اگر پنج است، پنجی که در کامپیوتر این آقا است؟ یا پنجی است که در کامپیوتر آن آقا است؟ میگویید هیچکدام. این رقم پنج در عدد پی، طبیعی این پنج، رقم قرار میگیرد.
ولذا در آخر مباحثه جلسه قبل، فرمودند اگر ابعاد عالم مادی را بینهایت فرض بگیریم، خُب این را یک جایی جا میدهیم. آن هم بر بحثهایی متفرع بود که چندین سال قبل بهصورت تفصیلی صحبت شده. اگر بهعنوان اصل موضوعی –نه بهعنوان یک امر محقق- فرض بگیریم عالم در بینهایت بزرگ شدن و بینهایت کوچک شدن، طرفین آن را مانند خطی فرض بگیریم که دو طرفش بینهایت باشد؛ خط باشد، نه نیمخط یا پارهخط. همین جور اگر برای بزرگ شدن و کوچک شدن، لبهای فرض نگیریم، هیچ مانعی ندارد. یک عالم اینچنینی را فرض گرفتهایم. اما این عالم فیزیکی که در بینهایت بزرگ و بینهایت کوچک فرض گرفتهایم واقعاً غیرمتناهی است، درعین حال، نمیتواند این عدد پی را سامان بدهد. چرا؟ بهخاطر اینکه وقتی شما میخواهید در محل فیزیکی، این بینهایت عدد را ذخیره کنید، ولو بسترش بینهایت است، شما در محل فیزیکی چه چیزی را بهعنوان ذخیره قرار میدهید؟ میخواهید بگویید رقم دوم [بعد از ممیز] عدد پی، چهار است -سه و چهارده صدم- میخواهید این چهار را در یک مکان و یک جای فیزیکی جا بدهید، در این عالم یک مختصاتی دارد؛ ولو مختصات چند بُعدی دارد، ولی خلاصه میخواهید آن را جا بدهید. وقتی آن را جا میدهید، این، یک فردی از آن رقم میشود. یک فردی از سه و چهارده صدم میشود. خُب آن را از اینجا بردارید و به جای دیگر ببرید، رقم عوض میشود؟ نه. رقمی که در ارقام عدد پی است، طبایعِ عددِ این ارقام است، نه یک فردی که یک جا آن را ذخیره کنید. آنچه که ذخیره کردهاید، یک نمادی است که آن طبیعت را در اینجا نشان میدهد. این مطلبِ خیلی پر اهمیتی است.
بنابراین اولین سؤال این است: طبیعت را از دل فرد بِکَنید و بالا ببرید. سؤال دوم این است: طبیعت را از تاریخ، از بشر و از خلقت او بالاتر ببرید. عرض کردم این دو سؤال، سؤال مهمی بود. حالا به این شکل نگاه کنید.
{#ارشمیدس، #محاسبه_عدد_پی_با_رسم، #فرمول_محاسبه_عدد_پی، #رساله_محیطیه، #غیاث_الدین_جمشید_کاشانی، #گنگ_بودن_عدد_پی}
{۰۰:۲۴:۴۷}
وقتی شما [در تطبیق قطر روی محیط باز شده دایره روی محور،] قطر را روی محور میگردانید، سه بار میآید، اما اگر بار چهارم هم بگردانید، از محیط جلو میزند. پس پی، بین سه و چهار است. بعد، از نود و شش ضلعی و سه چهارده صدم که ارشمیدس رفته، شما بین عدد سه و چهار را اعشاری میکنید. آن را ده قسمت میکنید. عدد بعدی سه و یک دهم است. پس در بخش یک دهم میآید. فقط بین سه و چهار را به خط پایینی آوردیم و آن را ده قسمت کردیم، در آن ده قسمت داریم جای سه و یک دهم را تعیین میکنیم. یک دهم تعیین شد ولی هنوز به پی نرسیدهایم.
میدانید در زمان ارشمیدس عدد پی را با رسم، محاسبه میکردند. اولین کسی که در تاریخ عدد پی، به فرمول دست یافت، غیاث الدین جمشید کاشانی است. من سالها قبل این را در لغتنامه دهخدا دیدم. ایشان یک رساله محیطیه دارد که رساله عالی و تاریخی است. اول هم که [رسالهاش را] شروع میکند، سرتا پا متانت است و شکر خداوند متعال میکند؛ عالمی به این صورت است. بعد این رساله را میآورد. اولین کسی که برای محاسبه پی، فرمول ارائه داده، که امروزه از آن فرمول استفاده میشود، غیاث الدین جمشید کاشانی است. جلسه قبل گفتم هفتاد تریلیون [رقم عدد پی] محاسبه شده، آن برای این فرمولها است. ایشان خودش فرمول را کشف کرد ولی باید محاسبه میکرد. تا شانزده رقم حساب کرد که تا رقم سیزده یا چهارده درست بود. بعد، دیگر اشتباه کرد. محاسبات خیلی سنگینی دارد. رساله محیطیه او ظاهراً موجود است. نمیدانم به خط خودش است یا نه.
تا زمان ارشمیدس کثیر الاضلاعهای محیطی و محاطی را مدام کوچک میکردند تا به محیط، نزدیک شوند. بعد فهمیدند اگر کثیر الاضلاع محیطی و محاطی را تا بینهایت ریز کنید، جایی نمیشود که کثیر الاضلاع شما دقیقاً با محیط یکی شود. معنای گنگ بودن، همین است.
شاگرد: با تجربه فهمیدند به این صورت است؟
استاد: نه، ارشمیدس که فقط میخواست برسد. غیاث الدین جمشید کاشانی هم نمیدانست و میگفت چه بسا یک وقتی رسیدیم. گنگ بودن چیز مهمی است. لذا عرض کردم در قرن نوزدهم یا اواخر قرن هجدهم معلوم نبود، بعداً ثابت شد که عدد پی، گنگ است. یعنی برهان اقامه شد که نمیشود؛ اگر تا بینهایت بروید، نمیشود. با کارهایی که اینها انجام دادند، عدد بعدی، سه وچهارده صدم شد. یعنی بین سه و چهارده و سه و پانزدهم صدم است. اگر بگویید پس سه و چهارده صدم است، هنوز به آن نرسیدهاید. نقطه سه و چهارده صدم، معین است، اما نقطه پی نیست. اگر بگویید سه و پانزده صدم، از پی رد شدهاید. یعنی عدد پی دقیقاً بین سه و چهارده صدم است و سه و پانزده صدم. ببینید چقدر مهم است! اگر در سه وچهارده صدم، چهار را پنج کنید، از محیط رد شدهاید. یعنی این نقاط دقیقاً تعینی دارند که اگر عدد بعدی آن را عوض کنید، به هم میخورد؛ از محیط رد شدهاید.
خُب حالا بعدش چه؟ بین سه و چهارده صدم با سه و پانزده صدم، دوباره ادامه مییابد. خط بعدی، بین سه و صد و چهل هزارم با سه و صد و پنجاه هزارم است. کجا میرود؟ به صد و چهل و یک هزارم میرود. همینطور مسیرش را عرض کردهام. در خط پایینی که قرمز رنگ است پنجاه رقم، اعداد بعد از ممیز است که الآن در مرجعهای جهانی معمولاً پنجاه رقم را میآورند. پنجاه رقم، بعد از ممیز است. این ارقام تا بینهایت میرود. ولی تا بینهایت هم که میرود، باز کمتر از پی است. یعنی شما همچنان به نقطه محیط نمیرسید. چرا؟ چون این اعداد برای کثیر الاضلاع محاطی است. محاطی هم، هر چه بالا برود نمیتواند دقیقاً خود محیط شود. از آن طرف هم کثیر الاضلاع محیطی به پی نزدیک میشود. ما به التفاضل آن، به صفر میل میکند، اما هیچ وقت صفر نمیشود. این خط زیرین است. یک توضیحی هم عرض کردهام که آن توضیح هم همین است.
آن چه که الآن منظور من است، این است: خط پایین را نگاه کنید. از آن جایی که ٣ نوشته تا جایی که پی نوشته، در این فاصله تا الآن که برای بشر واضح شده چند رقم در این بین هست که نقطه معینی را تعیین میکند؟ بینهایت نقطه معین با رقم معین در این فاصله هست. این تعین را ما کشف میکنیم؟ ما که در این ارقام جلو میرویم، بهآنها میرسیم یا آنها را فرض میکنیم و قرارداد میکنیم؟ این دیگر برعهده کسانی است که سرشان میشود؛ هر کسی در این تأمل کند، تردید نمیکند که این ربطی به ما نداشته و نسبت دایره و محیط را که بشر درنیاورده است. نه اینکه بحثهای فلسفی را ندانم. فی الجمله آنها را میدانم. بحثهای فلسفی و اشکالات و حملاتی که به این میکنند، معلوم و معروف است. ولی آن چه که من عرض میکنم، این است: اگر ابتدا به بحثهای آنها مراجعه نشود و این بهخوبی تصور شود، دارد یک تعین ریاضی را وراء ذهن بشر و وراء افراد فیزیکی نشان میدهد. یعنی طبایع بینهایتی را در این مسیر جلوی چشم هر ناظری میآورد. از اینجا است که با آن چشم عقلانی که بینهایت را میبیند، میبیند این بینهایت یک جایی در عالم فیزیکی ذخیره نشده. این موطنی است که موطن اشیاء ریاضی است. موطنی است که اقیانوس در اقیانوس، لایتناهی است. در آن جا بینهایت به توان بینهایت، بینهایت داریم. آن عالم، عالمی است که تمانع در آن نیست. مشکلی در آن نیست. حضرت، تعبیر میکنند مقام علم است، البته نه علم خود خدای متعال. علمی که در الواح مسبوقه به ذات او، ظهور کرده.
{#عالم_تجرد_ریاضیاتی، #هوش_اشراقمحور، #موطن_اشراق}
{۰۰:۳۲:۱۷}
علی ای حال مهم این است که خدای متعال به ما یک چیزی داده که این را میبینیم. حالا سؤال ما این است: وقتی رقم صدم را کشف کردیم، الآن آن رقم صدم در ما بازتاب پیدا کرد؟ بیرون بود و یک تعینی داشت، ما به آن رسیدیم و آن در ما بازتاب پیدا کرد؟ یا وقتی به رقم صدم رسیدیم، تازه ایجاد شد؟ اگر ما به آن رسیدیم، پس یک عالم تجرد ریاضیاتی هست که آنجا، آن عدد، ثابت است؛ ما مدام زحمت میکشیم که به آن برسیم. و لذا هم اشتباه میکنیم. اشتباه یعنی چه؟ اگر ما خلق میکردیم که اشتباه معنا نداشت. اشتباه یعنی ما میرویم ولی نمیرسیم. پس آن هست، ما سراغش میرویم که به آن برسیم.
این یکی از چیزهای بسیار مهم است تا چشم نوع، باز شود. درجاییکه میگوییم هوش اشراقمحور داریم یعنی اصلاً موطن اشراق داریم. این بیانات نشان میدهد که در بیرون یک جایی هست و از آن جا اشراق میآید. اما اینکه به چه صورت است، بعداً بحث میکنیم. مثل رادیویی است که نمیدانیم گوینده بیرون از آن چه کار میکند. ولی فعلاً میدانیم که در محدوده رادیو نیست. آن صدایی که میآید القاء آن و اصل قذف آن از بیرون است. این اصل مقصود من است.
{#عدد_متعالی، #عدد_رسمپذیر، #عدد_معین_رسمناپذیر}
{۰۰:۳۳:۴۶}
شاگرد: در نمودار نوشته اید عدد متعالی، مقصودتان از متعالی چه بوده؟
استاد: عدد متعالی، عدد غیر جبری است و معادل رسمناپذیر است. ببینید رادیکال دو، گنگ است، اما رسمپذیر است؛ یعنی بشر میتواند با رسم هندسی، آن را روی محور نشان بدهد و بگوید اینجا است؛ این جذر دو است؛ ولو در محاسبه، تا بینهایت به آن نمیرسیم، اما نشانش میدهیم. اما اعداد متعالی غیر جبری، رسمناپذیر هستند. یعنی ولو شما بینهایت به عدد پی نزدیک میشوید، اما هیچ وقت نمیتوانید روی محور بگویید اینجا است؛ محال است. همه اینها الآن در فضای ریاضی ثابت شده است. رسمناپذیر است، ولی معین است. این مهم است. چون حد است. وقتی حد است یعنی معین است و نقطه نامعین نیست. حد این دو دنباله است. وقتی حد شد، حتماً خودش معین است. اما ما نمیتوانیم آن را نشان بدهیم. این خیلی جالب است. با اینکه میدانیم معین است، اما رسمپذیر نیست و نمیتوانیم آن را نشان بدهیم.