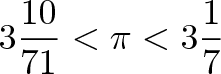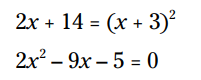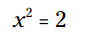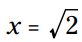فصل چهارم: عدد پی؛ بی‌نهایتِ در مشت

تحلیل اجزاء دایره

بی‌نهایت، انواعی دارد. یک مثال روشنش، عدد پی( )^[1] است. عدد پی، عددی هندسی است، یعنی شما اوّل سروکارتان با دایره می‌شود. دایره چیست؟ یک خطِّ بستهی منحنی. خط برای کجاست؟ برای هندسه است؛ کمّ متصل قارّ. دایره یک مرکز دارد. مرکز، نقطه است. نقطه، عنصر هندسی است. قطر چیست؟ خطّ مستقیمی که از مرکز رد می‌شود و دایره را دو قسمتش می‌کند. این خطّ مستقیم، طول است؛ کم متصل قارّ است.

عدد پی: نسبت محیط دایره به قطر

می‌خواهیم ببینیم نسبت محیط دایره به قطر چقدر است؟ یعنی اگر محیط را باز کنیم، از گِردی در بیاوریم و یک خطِّ مستقیمش بکنیم، چند تا قطر بگذاریم سر می‌رسد؟ می گوییم سه تا قطر را که روی محیط بغلطانید، دایره می گردد[2]، دفعه بعدش دیگر نه؛ کمی از آن فقط می‌ماند. این را می‌گوییم نسبت محیط به قطر، یعنی محیط، چند برابر قطر است؛ نسبت یعنی صورت، تقسیم بر مخرج. یعنی محیطِ گردِ دایره، تقسیم بر قطر، می شود عدد پی.فعلاً می‌گوییم ١۴/٣.

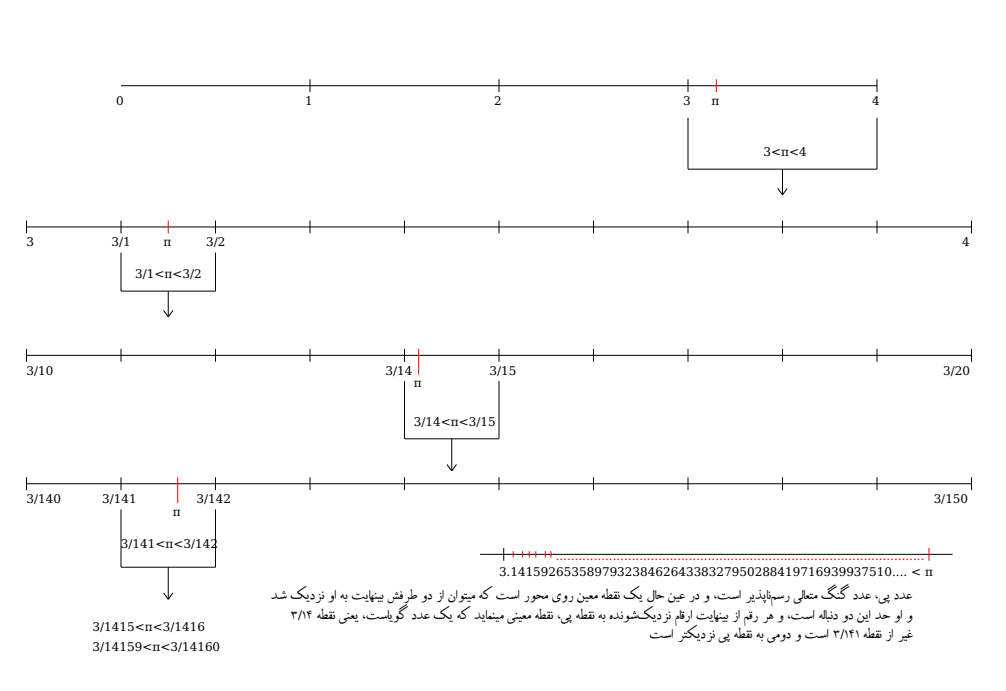
هر دایره دلخواه را –که دایره هندسی باشد- روی هر محوری رسم کنید، به محض این‌که روی محور اعداد، این دایره را باز کنید، اگر قطر این دایره،١ باشد(«یکِ» رویِ محور) یک سر محیط دایره را روی عدد صفر می‌گذارید، آن سرِ محیط می‌شود عدد پی^[3]. یک نقطهی معیّن روی محور؛سه و چهارده صدم و ...، بروید تا بی‌نهایت.^[4]

نسبت عدد پی: متجانسِ متباین

[آیا خط مستقیم با خط منحنی دو جنس هستند یا یک جنس هستند؟ خلاصه طول هستند. در اینجا روی یک نگاهی که همه دارند و پذیرفته شده است، خط منحنی با خط مستقیم از حیث کمّیت طول متجانس هستند، ولذا در دایره، محیط آن منحنی است اما قطرش خط مستقیم است؛ می‌گویید نسبت محیط دایره به قطر سه و چهارده صدم است. یعنی می‌توانید قطر را سه بار روی محیط دایره بغلطانید که مقادری هم زیاد می‌آید؛ سه و چهارده صدم. محیط سه برابر و خورده‌ای از قطر خودش است. قطر ضرب در سه و چهارده صدم نزدیک به محیط دایره می‌شود. خُب این نسبتی شد بین دو کمیت متجانس؛ نسبت محیط بر قطر.

این چه نسبتی است؟ متباین است یا متجانس است. این خیلی طول کشید. خُب قطر مربع دو هزار و پانصد سال پیش معلوم بود که متباین هستند. اما این‌که آیا قطر با محیط متباین هستند یا نه، تا حدود دویست سال پیش آمده است. یعنی این قدر در تاریخ طول کشیده تا بشر برهان بیاورد که نسبت محیط با قطر نسبتی است که تا بی‌نهایت می‌رود و اصم است؛ به یک عاد مشترک واحد نمی‌رسند[5].]

روش تحصیل عدد پی

عدد پی، عددی است که روی نقطه معیّنی روی محور است، اما شما نمی‌توانید نشانش بدهید. چه کار می‌کنید؟ از پس و پیش، به آن نزدیک می‌شوید. یعنی از ۳.۱۴ که مثلاً با ۹۶ ضلعی ارشمیدس بوده^[6]، از نقطه‌ ۳.۱۴ شروع می‌کنید، بعد از ۳.۱۴ روی محور، ۳.۱۵ است. می‌گویید نقطه پی که محیط دایره است، بین ۳.۱۴ و ۳.۱۵ هست. نه بیرون از ۳.۱۵ است، نه عقب‌تر از ۳.۱۴ است؛ بین این دو تاست. از طرفین(۳.۱۵ و ۳.۱۴ )به آن نزدیک‌تر می‌شوید وتا بی‌نهایت می‌روید. حدّش^[7] هست. به تعبیر مسامحی می‌گوییم در بی‌نهایت به پی میل می‌کند.

امروز دیگر اینها از واضحات است، یعنی اهل خبره دو نفرشان هم در این اختلاف ندارند، امروز برای بشر، این که عدد پی عددی است گنگ^[8]، متعالی^[9]و رسم‌ناپذیر^[10] ^[11] ، این‌ها همه مبرهن شده است^[12].

کاربرد معارفی عدد پی

خوب دقت کنید. الآن عددهای بعد ۱۴ صدُم را؛ممیّزهای بعد ممیّز را، تا چندین تریلیون حساب کردند^[13]. خلاصه آخرین عددی که فعلاً بشر می‌داند، می‌دانیم یک عددی معیّن بعدش هست؛ ما نمی‌دانیم، ولی معیّن است. ما باید برویم کشفش کنیم؛ نه فرضش کنیم؛ نه خلقش کنیم .نکته اصلی این است، این نقاطی که شما بعد از ممیّز می‌گذارید، نقطه‌ای معیّن روی محور است؛ نقطهی نامعین نیست. یعنی ۳.۱۴ که معین است، عدد بعدی ممیز که ۳.۱۴۱، روی محور معلوم است، ولو نزدیک‌تر به پی شده ولی خود پی نیست. عدد بعدی هم همین‌طور، تا بی‌نهایت می‌روید ولی به سر دایره نمی‌رسید، چون عدد گنگ است. ولی نقاطی که طی می‌کنید تا به آن نزدیک بشوید نقاط متعین است.

بی نهایت؛ قابل ارائه به بچه دبستانی

این است که می‌گویم زمینه‌اش فراهم است که برای بشر نشان بدهیم. الآن شما یک دایره را باز کردید، کف دست بچه می‌گذارید. می‌گویید این سر «پی» که معلوم است، صفر هم معلوم است. وقتی می‌خواهی حساب کنی بروی برسی به سر دایره که پی است، در رسیدن به نقطهی پی، بی‌نهایت نقطهی متعیّن است که هر چه حساب پی را جلوتر ببرید کشفش می‌کنید.دو طرف، بی‌نهایت. یعنی از دو طرف دارید به آن نقطه پی نزدیک می‌شوید تا بی‌نهایت هم در بی‌نهایت نزدیک می‌شوید، نقاطش هم متعین است، شما کشفش می‌کنید؛ ولی در عین حال هیچکدام از آنها «پی» نیست!این،یک مثالِ هندسیِ ساده است، هر بچه‌ای هم در دبستان خوانده است. می‌خواهیم چیزهایی را که همه بلد هستند فقط به او نشان بدهیم.

الان این مثال،مثل سنگ خاراست، فقط باید کار بشود و این مثال‌ها باز بشود،تصویری توضیح داده بشود، که همه بفهمند. وقتی اذهان مطلب را گرفتند، همین‌طور دست به دست می‌شود؛ به سرعت پخش می‌شود.

[1] عدد پی (π) (به انگلیسی: Pi) از عددهای ثابت ریاضی و تقریباً برابر با ۳٫۱۴ است. این عدد را با علامت π نشان می‌دهند. عدد پی عددی حقیقی و گُنگ است که نسبت محیط دایره به قطر آن را در هندسهٔ اقلیدسی مشخص می‌کند و کاربردهای فراوانی در ریاضیات، فیزیک و مهندسی دارد. عدد پی همچنین به ثابت ارشمیدس نیز معروف است .پی،حرف اول کلمهٔ یونانی «پریمتروس» (به معنی محیط) است.(سایت ویکی پدیا)

[2] گشتن به‌معنای دور زدن و نه به‌معنای شدن

[3]

[4] پویانمایی نسبت عدد پی به دایره را در سایت ویکی پدیا مشاهده نمایید.

[5] افاده شده در جلسه هشتم فقه هوش مصنوعی تاریخ 2/ 9/ 1402

[6] ارشمیدس محیط دایره را نمی‌دانست؛ اما ناامید نشد و از آنچه می‌دانست یعنی محیط یک مربع آغاز کرد. البته او در واقع با یک شش‌ضلعی محاسبه خود را آغاز کرد؛ اما از آنجا که ترسیم و کار کردن با مربع آسان‌تر است، ما از مربع استفاده می‌کنیم.

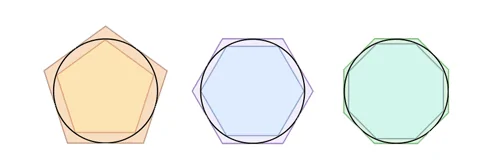
ما محیط یک دایره را نمی‌دانیم؛ اما می‌توانیم آن را بین دو مربع[محیطی و محاطی] رسم کنیم: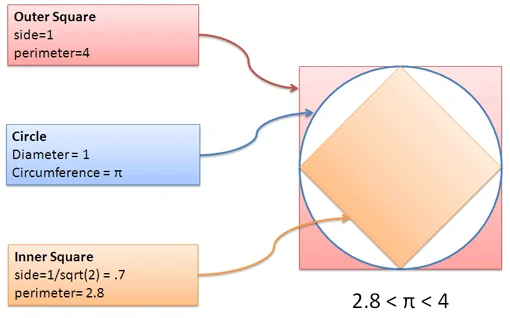

دقت کنید که این وضعیت شبیه مسیر مسابقه‌ای با یال‌های داخلی و خارجی است. محیط دایره هر چه که باشد بین محیط دو مربع قرار دارد، یعنی بیشتر از محیط مربع داخلی و کمتر از محیط مربع بیرونی است.محیط مربع‌ها را می‌توانیم به سادگی محاسبه کنیم:ما نمی‌دانیم که پی چقدر است؛ اما می‌دانیم که عددی بین 2.8 و 4 است. اگر تصور کنیم دقیقاً نیمه این دو کرانه باشد، پس باید در حدود 3.4 باشد.

مربع‌ها گوشه‌دار هستند. آن‌ها را نمی‌توان چندان شبیه دایره دانست و این اختلاف موجب محاسبات نادرست و با اشتباه زیاد می‌شود؛ اما با افزایش اضلاع، برای مثال با استفاده از هشت‌ضلعی می‌توانیم حدس بهتری از عدد پی داشته باشیم.

نان که می‌بینید با افزایش تعداد اضلاع، به شکل یک دایره نزدیک‌تر می‌شویم. متأسفانه اعداد اعشاری در سال 250 قبل از میلاد هنوز اختراع نشده بودند، چه برسد به نرم‌افزارهای صفحه گسترده. بنابراین ارشمیدس مجبور بود که این فرمول‌ها را به کمک کسرها حل کند. او کار خود را با شش‌ضلعی آغاز کرد و با ١٢، 24، 48 و 96 ضلع ادامه داد. تخمین نهایی وی از عدد پی با استفاده از شکلی با 96 ضلع به صورت زیر بود:

نقطه میانی این بازه برابر با 3.14185 است که تقریباً 99.9% دقیق است!(سایت فرادرس،مقاله عدد پی چگونه کشف شد؟)

[7] حد (به انگلیسی:( Limit): وقتی که مقادیر متوالی به یک متغیر نسبت داده می‌شود، و آن متغیر بی‌نهایت به عدد ثابتی نزدیک شود، به طوری که اختلاف آن‌ها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر می‌گویند.(سایت ویکی پدیا)

[8] عدد غیر نسبی، گُنگ یا اصم به انگلیسی:( Irrational number) در دستگاه اعداد به‌صورت عددی حقیقی تعریف می‌شود که عدد نسبی (عدد گویا) نباشد، یعنی نتوان آن را به صورت کسری نوشت که صورت و مخرجش عدد صحیح باشند.(همان)

[9] عددی که جبری نباشد، عدد متعالی یا ترافرازنده یا غیرجبری نامیده می‌شود.

نمونه‌های برجسته‌ای از اعداد ترافرازنده π و e می‌باشند. نمونه‌های کمی از اعداد ترافرازنده شناخته شده‌اند چرا که اثبات ترافرازنده بودن یک عدد دشوار است. با این حال، شمار آن‌ها کم نیست و تقریباً همهٔ اعداد مختلط و حقیقی ترافرازنده شمرده می‌شوند.

نخستین اثبات وجود اعداد ترافرازنده (متعالی) را جوزف لیوویل، ریاضی‌دان فرانسوی، در سال ۱۸۴۴ داده است.

(سایت ویکی پدیا، مدخل اعداد متعالی در این صفحه همچنین طبقه بندی اعداد را می توانید مشاهده کنید.)

اعداد گنگ دو نوع دارند: اعداد جبری (algebraic numbers) و اعداد متعالی (transcendental numbers)
مجموعه اعداد گنگ (Irrational Numbers)

به یک معنا، اعداد گنگ یک نوع خیلی فراگیر می باشند، هر عددی در خط اعداد که یک عدد گویا نباشد، یک عدد گنگ است.

با این تعریف، هیچ عدد گنگی نمی تواند به صورت کسری نمایش داده شود، همچنین یک عدد گنگ نمی تواند به شکل یک عدد اعشاری مختوم (terminating decimal) یا به شکل یک عدد اعشاری متناوب (repeating decimal) نمایش داده شود. (برای اطلاعات بیشتر در مورد این انواع اعداد اعشاری، فصل 11 را ببینید).

در عوض، یک عدد گنگ می تواند تقریبی از یک عدد اعشاری نامتناهی (non-terminating)، و غیر تکرار شونده (non-repeating) باشد:

یک رشته از اعداد بعد از ممیز اعشاری که بدون ایجاد یک الگو می توانند تا ابد ادامه پیدا کنند.

مشهورترین مثال از اعداد گنگ عدد پی (π) می باشد، که نماینده محیط یک دایره با قطر 1 واحد می باشد. یک عدد گنگ رایج دیگر 2√ می باشد، که نماینده طول قطر یک مربع با اندازه ضلع 1 واحد می باشد. در واقع، تمامی ریشه های توان دوم (square roots) از اعداد غیر مربع (non-square numbers) - مانند 3√، 5√، و به همین ترتیب - اعداد گنگ می باشند.

اعداد گنگ فضاهای موجود در خط اعداد حقیقی (real number line) را پر می کنند. (خط اعداد حقیقی همین خط اعدادی است که شما استفاده می کنید، اما متوالی است، هیچ جای خالی در آن وجود ندارد بنابراین هر نقطه ای بر روی آن با یک عدد جفت شده است.) اعداد گنگ در بسیاری از موارد که در آن نیاز به سطح دقت خیلی بالایی ندارید به شکل اعداد گویا مورد استفاده قرار می گیرند، اما مقدار دقیق آن عدد نمی تواند به صورت یک کسر نمایش داده شود.

اعداد گنگ دو نوع دارند: اعداد جبری (algebraic numbers) و اعداد متعالی (transcendental numbers). در مورد این دو نوع در ادامه همین فصل توضیحاتی را خواهم داد.

مجموعه اعداد جبری (Algebraic Numbers)

برای درک اعداد جبری، نیاز به اندکی دانش در مورد معادلات چند جمله ای (polynomial equations) دارید. یک معادله چند جمله ای، یک معادله جبری است که مطابق شرایط زیر باشد:

عملیات های آن محدود به جمع، تفریق، و ضرب باشد. به عبارت دیگر، لازم نیست که بر یک متغیر تقسیم کنید.

متغیرهای آن تنها به توان اعداد مثبت که در مجموعه اعداد کامل (whole-number) باشند، رسیده است.

شما می توانید در کتاب Algebra For Dummies اطلاعات بیشتری در مورد چندجمله ای ها بدست آورید.

در اینجا چند معادله چند جمله ای می بینید:

هر عدد جبری به عنوان راه حل حداقل یک معادله چند جمله ای، نشان داده می شود. برای مثال، فرض کنید معادله زیر را دارید:

شما می توانید این معادله را به شکل زیر حل کنید:

بنابراین 2√ یک عدد جبری می باشد که مقدار تقریبی آن برابر با ...1.4142135623 است.

مجموعه اعداد متعالی (Transcendental Numbers)

یک عدد متعالی (transcendental number)، در مقایسه با یک عدد جبری، هرگز راه حل یک معادله چند جمله ای نمی باشد. مشابه اعداد گنگ، اعداد متعالی نیز یک نوع فراگیر هستند: هر عددی در خط اعداد که عددی جبری نباشد، یک عدد متعالی است.

مشهورترین عدد متعالی π می باشد، که مقدار تقریبی آن برابر با ...3.1415926535 است. استفاده از این عدد در هندسه آغاز شد اما تقریباً به تمامی نواحی ریاضی گسترش یافت.

سایر اعداد متعالی مهم در هنگام مطالعه مثلثاث (trigonometry) برایتان پیش می آیند. سینوس ها (Sines) ، کسینوس ها (cosines)، تانژانتها (tangents) و سایر توابع مثلثاتی معمولاً اعداد متعالی می باشند.

یکی دیگر از اعداد متعالی مهم عدد e می باشد، که مقدار تقریبی آن ...2.7182818285 است. عدد e مبنای لگاریتم طبیعی (natural logarithm) می باشد، که احتمالاً تا زمانی که وارد مبحث حساب دیفرانسیل و انتگرال (calculus) نشوید، از آن استفاده نخواهید کرد. مردم از e برای حل مسائل مربوط به بهره مرکب (compound interest)، رشد جمعیت (population growth)، فروپاشی رادیو اکتیو (radioactive decay)، و مواردی از این دست، استفاده می کنند.(سایت خوشآموز،مقاله ده مجموعه مهم اعداد که باید بشناسید)

[10] در جبر و هندسه، عددی حقیقی r عدد ترسیم‌پذیر (انگلیسی: Constructible number) است اگر و تنها اگر بتوان با داشتن پاره‌خط واحد، با خط‌کش و پرگار بتوان در تعداد مراحل متناهی پاره‌خطی به طول |r| رسم کرد. تمام اعداد حقیقی ترسیم‌پذیر نیستند و برای توصیف آنهایی که ترسیم‌پذیر هستند باید از روش‌های جبری استفاده کرد.

یک نقطه در فضای دوبعدی ترسیم‌پذیر است اگر نقطهٔ پایانی پاره‌خط واحد باشد، یا نقطهٔ تقاطع دو خط که با نقاط ترسیم‌پذیر تعریف شده‌اند، یا تقاطع خط و دایره‌ای که مرکزش نقطه‌ای تقسیم‌پذیر باشد و از یک نقطهٔ تقسیم‌پذیر بگذرد، یا تقاطع دو تا از این دایره‌ها.

به‌عبارت جبری، یک عدد ترسیم‌پذیر است اگر و تنها اگر بتوان آن را با اعمال مراحل متناهی چهار عمل اصلی و ریشه دوم (فقط ریشهٔ دوم و نه ریشه‌های بالاتر) بر اعداد ترسیم‌پذیر دیگر ساخت، و ۰ و ۱ بنابر تعریف تفسیر پذیرند.(سایت ویکی پدیا، مدخل عدد ترسیم پذیر)

عدد a را «رسم پذیر» گوییم اگر بتوان تنها با استفاده از خط کش و پرگار پاره خطی به طول a رسم کرد. و البته فرض ما بر این است که یک واحد طول داده شده باشد.از این به بعد هر جا کلمه رسم پذیری آمد منظور همان، رسم پذیری به وسیله خط کش و پرگار است.رسم پذیری بعضی عددها بسیار واضح است. مثلا ۱ و ۲ و ... اما بعضی دیگر احتیاج به بررسی دارند مثل 2√ . آیا این عدد رسم پذیر است؟

از دوران دبیرستان به یاد داریم که : از هر نقطه خارج یک خط مفروض می توان خطی عمود بر آن رسم کرد.اگر محل تلاقی این دو خط را مبدأ،در نظر بگیریم به این محور، محور رسم پذیر می گوییم.

در این محور:

۱(a,0)يا(0,a) را رسم پذیر گوییم اگر a رسم پذیر باشد.

۲) (a,b) را رسم پذیر گوییم اگر a و b رسم پذیر باشند.

هر شکلی را که روی این محور بتوان رسم کرد، اعم از پاره خط، دایره و... یک شکل رسم پذیر گوییم.

حال می توانیم به راحتی بگوییم که 2√رسم پذیر است. چون اگر(۰.۱)و (۰و۱) را روی محور به هم وصل کنیم بنابر قضیه فیثاغورث پاره خطی به طول 2√داریم. حال سوالی که مطرح می شود این است که آیا همه اعداد رسم پذیرند؟ و اگر نه چه عددهایی رسم پذیرند و کدام ها رسم پذیر نیستند. همه عددها رسم پذیر نیستند و تعیین رسم پذیری آنها به کارهای تخصصی می‌انجامد.

حال سوالی که مطرح می شود این است که آیا همه اعداد رسم پذیرند؟ و اگر نه چه عددهایی رسم پذیرند و کدام ها رسم پذیر نیستند. همه عددها رسم پذیر نیستند و تعیین رسم پذیری آنها به کارهای تخصصی می انجامد اما حالا که مفهوم عدد رسم پذیر رو فهمیدیم چند حکم کلی درباره رسم پذیری رو هم بیان می کنیم:

۱) اگر a و b رسم پذیر باشند آنگاه a+b , a b , a.b , a/b نیز رسم پذیرند.

۲) اگر a رسم پذیر باشد آنگاه رادیکال a نیز رسم پذیر است.

۳) موارد زیر معادلند (یعنی اگر یکی از آنها در مورد یک عدد درست باشد دو تای دیگر نیز درستند):

الف) x رسم پذیر است.

ب) (Cos(x رسم پذیر است.

ج) (Sin(x رسم پذیر است.

۴) همه اعداد گویا (Q) رسم پذیر هستند.

اکنون کار قضاوت در مورد رسم پذیری عددها خیلی ساده تر شد. تنها عددی ممکن است رسم پذیر نباشد که گنگ باشد. اما تعیین اینکه عدد گنگی رسم پذیر است یا نه دارای تکنیکهای ویژه ایست.

.(سایت آی هوش، مقاله رسم پذیر بودن یک عدد)

[11]

[12] در سال ۱۷۶۱ لامبرت ریاضیدان سوئیسی ثابت کرد که عدد پی گنگ است و نمی‌توان آن را به صورت نسبت دو عدد صحیح نوشت. همچنین در سال ۱۸۸۲ فردیناند فون لیندمان ثابت کرد که عدد پی یک عدد جبری نیست و نمی‌تواند ریشه یک معادله جبری باشد که ضرایب آن گویا هستند. (همانند عدد (e))کشف گنگ بودن عدد پی، به سال‌ها تلاش ریاضی‌دانان برای تربیع دایره پایان داد.(سایت ویکی پدیا)

[13] باوجود آنکه همه ریاضی‌دانان می‌دانند که عدد پی گنگ می‌باشد و هرگز نمی‌توان آن را به‌طور دقیق محاسبه کرد اما ارائه فرمول‌ها و مدل‌های محاسبه عدد پی هموار برای آن‌ها از جذابیت زیادی برخوردار بوده‌است. بسیاری از آن‌ها تمام عمر خود را صرف محاسبه ارقام این عدد زیبا نمودند اما آن‌ها هرگز نتوانستند تا قبل از ساخت کامپیوتر این عدد را بیش از ۱۰۰۰ رقم اعشار محاسبه نمایند. امروزه مقدار عدد پی با استفاده از پیشرفته‌ترین رایانه‌ها تا میلیون‌ها رقم محاسبه شده‌است؛ و تعداد این ارقام هنوز در حال افزایش است.

اولین محاسبه کامپیوتری در سال ۱۹۴۹ انجام گرفت و این عدد را تا ۲۰۰۰ رقم محاسبه نمود و در اواخر سال ۱۹۹۹ یکی از سوپر کامپیوترهای دانشگاه توکیو این عدد را تا ۲۰۶٬۱۵۸٬۴۳۰٬۰۰۰ رقم اعشار محاسبه نمود. (سایت ویکی پدیا)

آخرین رقم اعشار محاسبه شده، به عدد ۳۱ تریلیون رسیده است.