فصل پنجم: عدد پی؛ ابزار ارائه مجرّدات

آیا وقتی شما می‌گویید یک دایره محیطش با قطرش، نسبتی دارد، واقعاً این شکل(شکل دایره که یک خط است و این نقطه مرکزش است) چه کسی است که آن را به وضوح درک نکند؟ همه می‌فهمیم شکل چیست؛ درک روشنی از آن داریم.

سؤال این است:

سؤال: عدد پی؛ نسبتِ کدام دایره؟

- وقتی می‌گوییم نسبتِ دایره به قطر، منظور ما از این دایره، کدام دایره است؟ دایره‌ای است که فقط در ذهن شماست یا در ذهن من است؟ دایره‌ای که در دفترِ شما کشیدند یا دایره‌ای که در دفترِ من کشیدند؟ کدام دایره؟ همه­ی این ها روی هم؟

یعنی اگر هر چه دایره­­ی کشیده هست یا ذهن‌های همه بشر یک دفعه محو بشوند، نسبت محیط دایره به قطرش تمام می‌شود؟ این‌که محیط دایره سه برابر قطرش است، این نسبت دیگر نیست؟ محو می‌شود؟ یا نه؛ ذهن و عقل ما این نسبت را درک می‌کند.

اگر هیچ انسانی نباشد، ولی یک شیئ تیزی بیاید و  یک سنگی را که به صورت گردی هست ببرد، مقطع این سنگِ گردِ توپ­مانند، دایره نیست؟ دایره­ی مادّی. اتصاف او به این گِرد بودن به ذهن ما ربطی دارد؟

وقتی شما یک توپ را نصف می‌کنید، نصف شدن توپ، بند به ذهن شما نیست. و حدوث مقطع یک توپ به عنوان سطحِ دایره، باز به ذهن شما مربوط نیست. یعنی شما  می‌توانید دایره‌ای در بطن ماده پیدا کنید.الان من چیزی را درک می‌کنم گرد است یا من به آن می‌گویم گرد است؟ اگر گفتن است ،بگویید مربع است؛ یک اقوامی بگویند این چهارگوش است، یک اقوامی بگویند گرد است.

مفهومِ طول؛ چند متر؟

 شما می‌گویید: محیط، قطر، دایره، طول، فاصله، بُعد. وقتی طول می‌گویید، همه می‌فهمند: طول یک متری، یک سانتی‌متری، یا  بُعد: بُعد ۲ سانتی مثلاً.

وقتی می‌گویید طول،  آیا مفهوم طول،هم طول دارد یا ندارد؟ چند متر است؟ طول، دیگر معنایش طول ندارد، اما مصداقش چرا، طول دارد.

ابتدا و انتهای مفهوم فاصله؟

فاصله؛ هر فاصله‌ای بینش دو نقطه است. هر فاصله‌ای اوّل دارد، آخر دارد، دو طرف دارد. آیا مفهوم فاصله هم دو طرف دارد یا ندارد؟ مفهومِ فاصله، دو تا لبه ندارد؛ مصداقش است که دو تا لبه دارد. مفهوم فاصله، در آن فاصله نیست. این ها مفاهیم‌اند.

شعاع دایره؛ مفهوم فاصله یا مصداق فاصله؟

وقتی شما می‌گویید که فاصله­ی بین مرکز دایره با محیط دایره، شعاع دایره است. الآن آیا این فاصله‌ای که شما به کار بردید، مفهومِ فاصله است یا مصداق آن است؟ این فاصله، مفهوم نیست؛ چون اوّل و آخر آن، دو تا نقطه است-از مرکز تا محیط دایره-واقعاً بین این دو، فاصله­ی خارجیِ مصداقی است. اما اگر مصداق است پس چرا تعیّن ندارد؟ شما مفهوم کلی فاصله را طوری در نظر گرفتید که با افراد مختلف، صدق کند.

پاسخ: عدد پی؛ نسبت سنجی در کلّی دایره

قطر، محیط، دو تا مفهوم‌اند. نسبت بین این دو تا مفهوم از نسب اربعه چیست؟ تباین است؛ هیچ قطری محیط نیست و  هیچ محیطی هم قطر نیست. این از حیث مفهوم، روشن است. دوباره شما می‌گویید نه. من که می‌گویم نسبت بین محیط با قطر، مقصودم بین دو تا مفهوم از حیث مصادیقشان نیست که می‌گویید متباین‌اند؛ من در یک دایره، نسبت سنجی می کنم. همین جا آیا باید دایره­ی مشخصی باشد تا نسبت برقرار بشود؟ یا نه؛ در کلّیِ دایره بین محیط با قطر، نسبت برقرار می‌شود. کلّی به کلّی.

سؤال: عدد پیِ کلّی؛ دارای شکل؟

سؤال ما دقیق این است:

الآن که نسبت بین محیط با قطر کلی‌ است، این قطر، این محیط و این نسبت این دو، به همین نحوی که الآن برقرار است، دارای شکل هستند یا نیستند؟ آن هایی که طرف نسبت‌اند، آن ها شکل دارند یا ندارند؟ اگر شکل دارند، مقدار باید داشته باشند. مقدارشان چه اندازه است؟ نامتعین است؟چطور شما یک شکلی دارید که اندازه‌اش نامتعین است. مگر ما شکل کلی هم داریم؟

الف) پاسخ ابتدایی: مراتب شکل

١. شکل عقلانی: مفهوم بدون شکل

اصلاً شکل یک مفهوم عقلانی دارد. شکل، شکل ندارد. شکل، یک مفهوم کلی است.

٢. شکل مثالی منفصل: بدون تعیّن

 اما مصداقش، یک دایره می‌شود. دایره، یک شکل است به حمل شایع. تفاوت این دو تا چیست؟ تفاوتش این است که شکل دایره به عنوان یک شکل، از عالم مثال منفصل است و لذا بین الاذهان است؛ همه­ی اذهان با هم در یک عالمی می‌روند که در منظر همه بشر است و آن را می‌بینند. آن عالم کجاست؟ مثال منفصل؛ مجرّد است به تجرد برزخی، آثار ماده را دارد ولی خود ماده را ندارد.

دایره ۲ متری، به ذهن شما بند است. دایره ۳ متری هم به ذهن دیگری بند است. اما شکل  دایره -نه کلّیِ شکل که عقلانی است- شعاعش چقدر است؟ شکل دایره، قطرش چند متر است؟ اتفاقاً آن هایی که هندسه درس می‌دهند می‌گویند دایره‌ای با قطر واحد، یا دایره‌ای با شعاع واحد. پس در علم هندسه به راحتی شکل دایره را درک می‌کنند. شکل هست، ولی تعیّنِ مقدارِ خاصّی از شعاع و قطر نداریم.

٣. شکل مثالی متصل: متعیّن

 به محض این‌که یک دایره را شعاع مِتریک به آن بدهید، بگویید ۲ متر، ۳ متر، متشخّص شد؛ شد یک فرد دایره‌ای که در قوه­ی خیالِ متصل موجود است. یعنی ذهن شما یک شعاع خاصی را به آن داد، حالا شد خیال متّصل.

پس شکلِ دایره، شکلِ مربع، یک طبیعی است که خودش را در ضمن کمّ متصل قارّ در عالمِ مثالِ منفصل به ذهن ما نشان می‌دهد. اما ما چون الآن داریم او را به راحتی می‌بینیم، مثل بچه‌ای هستیم که هنوز تشخیص نمی‌دهیم که آن شکل منفصل برای عالم مثال منفصل، با آن شکل برای مثال متصل که تصور می‌کنم تفاوت دارد.

-ما عالم مثالی که می‌شناختیم  و در درس خوانده بودیم، فرد بود. عالم مثال هم فرد دارد و هم طبیعی[1]؟

اینجاست که قدر این روایت  را می‌دانید؛ خود عالم مثال، ۱۸۰۰۰ عالم است^[2]. ما هنوز می خواهیم با یک زحمتی دوتایش را  تفکیک کنیم. ۱۸۰۰۰ عالم است. عوالم با هم فرق دارند.

من نمی‌خواهم چیزی را ثابت کنم. می‌خواهیم آن چیزی که همه داریم ببینمش. ما وقتی در هندسه می‌گوییم نسبت محیط به قطر، محیط قطعاً کم است، خط است، طول است. اما چند متر؟ طولی است که متر فیزیکی ندارد. نمی‌خواهیم بگوییم چند متر است. قطعاً طول است، قطعاً تجرد تام نیست. چرا؟ چون طول شکل دارد و در قوه خیال ظاهر می‌شود. شکل دایره در قوه خیال حاضر می‌شود. اما این شکل دایره‌ای که احضارش می‌کنید، شما با عقلتان در مثال منفصل شکل دایره را می‌بینید. چند متر است؟ مثال منفصل، متر نمی‌خواهد. طول می‌خواهد، خط منحنی می‌خواهد، اما اندازه نمی‌خواهد. وقتی به عالم فیزیکی می‌آید اندازه می‌خواهد.

اشکال: ابهام در عالم مثال؟

ما طول مبهم داریم یا نداریم؟ این‌که همین ابهام سبب بشود برای نفی چنین صورتی در عالم مثال منفصل و ما بگوییم قطعاً این طول در عالمِ مثالِ منفصل نیست، این ملازمه و سببیّت برقرار نیست.

به خاطر این‌که عوالمی در مثال منفصل هست-این­طور که گفته اند و مدعی شده اند- که آن تفرّدِ فیزیکیِ خارجی را خیلی نیاز ندارد. یادم می‌آید مرحوم میرزا جواد آقا ملکی تبریزی فرموده بودند که به یک میوه وقتی در عالم مثال نگاه می‌کنید، میوه در عین حال که سیب است، در همان حال پرتقال است. این برای ذهن ما الآن سنگین است.^[3]روایت هم دارد. ذیل بحث میوه ممنوعه‌ای که حضرت آدم(علیه السلام) خورده است، بعضی می‌گویند خرما است، بعضی می‌گویند گندم است، انگور است حضرت فرمودند که همه این ها هست^[4].

 خلاصه نمی‌شود احکامِ اینجا را بر آن ها جاری کرد. یک میوه را وقتی نگاهش می‌کند، هم سیب است هم پرتقال است. ما الآن می‌گوییم معقول نیست؛ تناقض می‌شود؛ اجتماع ضدین می‌شود.این را فقط اشاره مطرح کردم که این­طور ادّعا و نظر هست که عالم منفصلی از مثال داریم که خیلی احکامی که اینجا داریم، لازم نیست آنجا باشد. و لذا دایره‌ای که طولش مبهم است، در آنجا یک امر محالی نیست، ولی در عین حال شکل است، طول دارد؛ خواص ماده را دارد، ولی مادّیت مادّه را ندارد.

ب) پاسخ نهایی: بررسی یک احتمال

مثال‌های ما این را واضح کرده که  شکل دایره، حتماً یک واقعیت منفصلی دارد، ولی این واقعیت منفصل تجرّد برزخی دارد؟ یعنی آثار ماده از شکل و طول و عرض و رنگ دارد که مثال منفصل بشود؟ یا نه، آن واقعیتی که دارد از سنخ معناست؛ از سنخ معنایی که به قوه خیال ما این طول و عرض و خواص مادّه را دستور می‌دهد.

عدد پی کلّی؛ معقول منفصل

تأمل کردم، دیدم احتمال قوی‌ای است- نمی‌شود از کنارش رد شد-که این شکل به عنوان یک موجودِ نفسی در ذهن ما اصلاً معنا نداشته باشد. یعنی ذهنِ من و شما همه ،یک معانی ای مرکب که همه‌اش از سنخ طبایع است، به عنوان فرمولی از معنا دارد که تا می‌گویید: «علامت جمع[5]»، فوری در قوّه­ی خیالتان، یک علامت جمع ترسیم می‌کند. راسِمَش، یک معنایی است که عقلتان درک کرده است. اگر آن معنای درکی را نداشتید، قوّه خیال شما، قوّه­ی این که آن را ترسیم کند نداشت.

عکس های اس وی جی (SVG)

عکس‌هایی هست که همه در موبایل‌هایتان دارید؛ از سنخ اس وی جی(SVG) ^[6]. اگر کد این ها را ببینید، جز چند تا فرمول هیچ چیز دیگری نیست، صفحه­ی مانیتور موبایلتان یا کامپیوترتان را تقسیم‌بندی کردید، با فرمول به آن می‌گویید این طور در مانیتور، عکس بکش، از اینجا به آنجا بکش. یک تصویر در می‌آید. ذهنِ ما در خزانه­ی معانی خودش، یک فرمولِ معنایی دارد، حتّی بچه‌ای که ‌در ذهنش، مثلّث می‌کشد، آن معناست که به او اجازه می‌دهد که بتواند در ذهنش یک مثلث رسم کند.

مثال‌هایش را هم شما شبیه این دستگاه های  امروزی ببینید، آن که در دلِ حافظه­ی کامپیوتر و موبایل است،  نقش نیست، در دل آن، هرگز علامت جمع نیست، اما یک فرمولی، یک نظمی در دل حافظه­ی او هست که نرم افزار وقتی به آن فرمول نگاه می‌کند، به صفحه نمایش دستور می‌دهد این علامت جمع را وضع کن. از نقطه­ی­ فلان بکش به نقطه دیگر؛نگاشت ریاضی.

نگاشت

لفظ نگاشت دو جا به کار می‌رود:

1.     لفظ نگاشت در فضای ریاضیات؛ تابعِ حوزه و دامنه[7].

2.     نگاشت یعنی تصویر به تصویر؛مثل نقشه­ی ایران کشیدن.

 این مفهوم دوم را نمی‌شود اینجا بگویند.مقصود ما در اینجا، نگاشت ریاضی[8] است. مثل این که  دستگاه شما آن چیزی که دارید در مانیتورش می‌بینید، فرق دارد با این دستگاهی که دیگری دارد در مانیتورش می‌بینند. گرچه  آن مطلبی که در حافظه دستگاه شماست، یکی است، ولی مانیتورها دو تاست، یعنی دستوری که دستگاه شما می‌دهد که نگاشت کن، در مانیتور با آن فرق می‌کند.

جمع بندی

با این حساب، برهانِ ما فعلاً اثبات نکرده که یک  نقشی منفصل داریم که آن را از مثالِ منفصل، احضار کنند و به چنگ بیاورند.

عدد پی؛ ابزار ارائه معنای منفصل

 ما آن را که به وضوح داریم، یک معنای منفصل^[9] است از آن نقش. این معنا  را من و شما، همه داریم. به محض این‌که به آن معنا توجه می‌کنیم، آن معنا در صحنه­ی  ذهن من و شما که به منزله مانیتور است، فوری می‌گوید یک بستر فراهم کن، رزلوشن درست کن، پیکسل‌هایش را بگذار، در آن پیکسل‌ها این ها را حذف کن. یعنی خود معنا این دستور را می‌دهد.

سؤالات ما فعلاً یک واقعیت این چنینی را به‌طور واضح، منفصل می‌کند. برایش اثبات می‌کند که شکی در آن نیست.منفصل یعنی اگر ما هم نبودیم، بود. انسان نبود، ذهن او هم نبود، این چنین بود. تمام کسانی که با مفاهیم هندسی و ریاضی آشنایی مختصر داشته باشند، حرف های ما را می‌بینند که در خودشان اینها را دارند ؛ نه این که  برایشان اثبات بشود، اما مثال منفصل را نه؛ هنوز تا این اندازه فاصله داریم که بتوانیم نشان بدهیم که ببین! ما یک نقش منفصل داریم که او را فراچنگ آوردیم، ولی ما به مقصودمان رسیدیم. چون برایمان کافی است که بگوییم پشتوانه­ی این نقش، یک معناست.

[1] سؤال یکی از دوستان حاضر در جلسه درس

[2]  سئل أمير المؤمنين صلوات الله عليه عن قول الله عز و جل: و كذلك نري إبراهيم ملكوت السماوات و الأرض‏ قال الأصبغ بن نباتة: كنت جالسا بين يديه مطرقا إلى الأرض، فرفع يده إلى فوق ثم قال لي صلى الله عليه: ارفع رأسك فطرقت رأسي، فرفعت رأسي، فرأيت السقف قد انفرج و رأيت نورا ساطعا إلى تحت العرش، فحار بصري فرددته، ثم قال لي صلى الله عليه: يا ابن نباتة، فرأى إبراهيم ملكوت السماوات و الأرض هكذا، ثم قال صلى الله عليه: أطرق رأسك فطرقت رأسي‏ ثم قال: ارفع رأسك، فرفعت رأسي و إذا السقف بحاله.ثم أخذ بيدي فقام و أخرجني من البيت الذي كنا فيه فأدخلني ببيت آخر و خلع ثيابا كانت عليه و لبس ثيابا غيرها، ثم قال: لا تفتح عينك، فلبثت ساعة ثم قال عليه السلام: تدري أين أنت؟ قلت: لا يا مولاي، قال صلى الله عليه: أنت في الظلمة التي سلكها ذو القرنين.فقلت له: جعلت فداك، أ تأذن لي حتى أفتح عيني؟فقال عليه السلام لي: افتح فإنك لا ترى شيئا، ففتحت عيني فإذا أنا في ظلمة لا أبصر فيها موضع قدمي، ثم سار قليلا و وقف و قال: أ تدري أين أنت؟ قلت: لا يا مولاي، قال عليه السلام: أنت واقف‏على عين الحياة التي شرب منها الخضر عليه السلام، و سرنا قليلا إلى عالم آخر فسلكنا فيها فرأيتها كهيئة عالمنا هذا في نباته و ساكنه و أهله، ثم خرجنا إلى عالم ثان حتى وردنا على خمس عوالم ثم قال صلوات الله عليه: هذه ملكوت الأرض كما ترى و هي ثمانية عشر ألف‏ عالم‏، كل عالم كهيئة ما رأيت.ثم أخذ بيدي فإذا نحن بالبيت الذي خرجنا منه، و نزع تلك الثياب و لبس ثيابه التي كانت عليه، و عدنا إلى مجلسنا، فقلت له: جعلت فداك، كم مضى من النهار؟فقال: ثلاث ساعات‏ (المناقب (للعلوي) / الكتاب العتيق، ص: 8۴-85)

[3] بعضى از خواص براى عالم مثال مطالبى بيان داشته‌اند كه براى اكثر مردم قابل قبول نيست، اينان براى گفته‌هاى خود از اخبار و رواياتى كه در حالات كاملين و صفات آنها رسيده استشهاد نموده‌اند از جمله اين فرمايش معصوم كه مى‌فرمايد: كلنا محمد. همۀ ما محمد هستيم و يا كلنا واحد. همۀ ما يكى هستيم، يا آن روايت كه مى‌گويد بعضى از نهرهاى بهشتى مشروباتى دارد كه طعم هر مطعوم و مشروبى در آن هست، اينان مى‌گويند اين بدان خاطر است كه هر موجودى از موجودات آن عالم در بردارندۀ همۀ خصوصيات موجودات ديگر آن عالم نيز هست، و لذا انسان در هر لحظه‌اى جميع لذاتى كه در همۀ موجودات آن عالم وجود دارد با طعم مخصوص، و لذت خاص آنها، در هريك از آن موجودات مى‌يابد بدون اينكه خصوصيتى از يكى از آنها از بين برود(اسرار الصلوه،١٣٠)

[4] قال الإمام أبو محمد العسكري (عليه السلام): ...فقال تعالى: و لا تقربا هذه الشجرة شجرة العلم، فإنها لمحمد و آله خاصة دون غيرهم، و لا يتناول منها بأمر الله إلا هم، و منها ما كان يتناوله النبي (صلى الله عليه و آله) و علي و فاطمة و الحسن و الحسين (عليهم السلام) بعد إطعامهم اليتيم و المسكين و الأسير، حتى لم يحسوا بعد بجوع و لا عطش و لا تعب و لا نصب.و هي شجرة تميزت بين أشجار الجنة؛ إن سائر أشجار الجنة كان كل نوع منها يحمل نوعا من الثمار و المأكول، و كانت هذه الشجرة و جنسها تحمل البر و العنب و التين و العناب‏و سائر أنواع الثمار و الفواكه و الأطعمة، فلذلك اختلف الحاكون لذكرالشجرة، فقال بعضهم: هي برة، و قال آخرون: هي عنبة، و قال آخرون:هي تينة، و قال آخرون: هي عنابة. (البرهان في تفسير القرآن، ج‏1، ص: 178)

در کتاب الثاقب فی المناقب ابن حمزه طوسی نیز چنین آمده است: فبينا نحن وقوف، إذ نحن بغمامة قد أظلتنا ببرق‏ و رعد حتى قربت منا، فألقت بين يدي رسول الله (ص) سفرة عليها رمان، لم تر العيون مثلها، على كل رمانة ثلاثة أقشار: قشر من اللؤلؤ، و قشر من الفضة، و قشر من الذهب.فقال (ص) لي: قل: بسم الله و كل يا علي، هذا أطيب من سفرتك. و كشفنا عن الرمان، فإذا فيه ثلاثة ألوان من الحب: حب كالياقوت الأحمر، و حب كاللؤلؤ الأبيض، و حب كالزمرد الأخضر، فيه طعم كل شي‏ء من اللذة (الثاقب في المناقب، ص:۵٨- 59)

در کافی شریف نیز در وصف رسول مکرم اسلام چنین آمده است:له حوض أكبر من بكة إلى مطلع الشمس‏ من رحيق مختوم‏ فيه آنية مثل نجوم السماء و أكواب مثل مدر الأرض عذب فيه من كل شراب و طعم‏ كل‏ ثمار في الجنة (الكافي (ط - الإسلامية) ؛ ج‏8 ؛ ص139)

[5] بحث از علامت جمع و ابعاد مختلف آن در مقاله«مثال دقیق، سؤال روان؛ ابزاری برای ارائه مجردات به همگان» قابل مشاهده است.

[6] در دنیای کامپیوتر دو نوع گرافیک برای عکس ها داریم : یکی Raster و دیگری Vector  .

درRaster Graphics که به آن گرافیک شطرنجی هم گفته می شود ، تصویر ها به صورت پیکسلی هستند ، طبیعتا هر کدام از این پیکسل ها رنگ خاص خودشان را دارند و جداگانه ذخیره می­شوند . همه ی فرمت های bmp، jpg ، و gif از این دسته هستند . ویژگی این مدل تصاویر این است که با بزرگ تر شدنشان، کیفیتشان کمتر می‌شود.

اما در Vector Graphics که به آن گرافیک بُرداری می­گویند  یک تصویر، مجموعه ای از نقطه ها ، خط ها ، منحنی ها و چندضلعی ها هست.  این نوع گرافیک با مختصات ریاضی سروکار دارد. تصور کنید یک محور x و y ترسیم شده و هرکدام از این بردار ها با متوجه به مختصاتی که دارند ترسیم شدند و سرجای خودشان قرار گرفتند ( منظور از بردار صرفا یک خط راست نیست ). در این روش، به مرورگر دستور می­دهیم در فلان نقطه، فلان بردار را ترسیم کن . در این مدل از تصاویر، کیفیت به اندازه وابسته نیست و به طور کلی مستقل از رزولوشن است .

اس وی جی مخفف عبارت Scalable Vector Graphic به معنای نگاره‌سازی بُرداری مقیاس‌پذیراست.نمونه یک تصویر SVG را در ادامه مشاهده می کنید.تصویر سمت چپ،نمونه دستورِ داده شده به رایانه و تصویر سمت راست،خروجی دستور به صورت تصویر است.(سایت ویرگول،‌مقاله اس وی جی چیه و چکار میکنه؟)

[7] به صورت ساده می‌توان بیان کرد که دامنه یک تابع، شامل تمام مقادیری است که به عنوان ورودی به تابع داده می‌شوند و برد تابع نیز مجموعه مقادیر خروجی از تابع را در بر می‌گیرد.

اما مهم‌ترین نکته‌ای که باید به آن توجه کنید این است که دامنه و برد، دو مفهوم اساسی در تعریف توابع هستند و با تغییر آن‌ها تعریف تابع نیز تغییر می‌کند. در ادامه این مطلب از مجله فرادرس، این موضوع به صورت دقیق مورد بررسی قرار می‌گیرد و تعریف جامعی از دامنه، برد و هم‌دامنه ارائه می‌شود.

همانطور که می‌دانید، یک تابع روی مجموعه‌ای از ورودی‌ها عمل می‌کند و مجموعه‌ای از خروجی‌ها را تولید می‌کند. بنابراین می‌توان بیان کرد که هر تابع از یک سری ورودی و خروجی تشکیل شده است. برای آنکه مفهوم این موضوع را به صورت دقیق متوجه شوید، به مثال زیر توجه کنید.

مثال

درختی که در شکل زیر نشان داده شده است هر سال به اندازه ۲۰ سانتی متر رشد می‌کند.

بنابراین می‌توان بیان کرد که ارتفاع درخت به میزان سن آن با استفاده از تابع h مرتبط است. این تابع را می‌توان به شکل زیر نمایش داد.

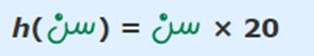
بنابراین در صورتی که سن درخت برابر با 10 سال باشد، ارتفاع آن مطابق با رابطه زیر، برابر با 200 سانتی متر خواهد بود.

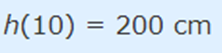
رابطه فوق را می‌توان اینگونه بیان کرد که تابع h، عدد 10 را به 200 تبدیل کرده است. بنابراین عدد 10 ورودی این تابع و 200 خروجی آن را نشان می‌دهد. این موضوع با استفاده از رابطه زیر نیز به خوبی نشان داده شده است.

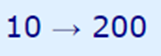
ورودی و خروجی یک تابع

نکته بسیار مهمی که باید به آن توجه کنید این است که، تمامی مقادیر و اعداد را نمی‌توان به عنوان ورودی به تابع معرفی کرد و اگر به تابع ورودی اشتباه بدهیم، ممکن است که تابع عمل نکند و هیچ خروجی را به ما تحویل ندهد.

دانستن اطلاعات کلی درمورد خروجی‌های تابع نیز امر بسیار مهمی است. برای مثال اگر بدانیم که این تابع تنها مقادیر مثبت را به عنوان خروجی به ما تحویل می‌دهد، درک مسئله برای ما بسیار ساده‌تر خواهد بود.

علاوه بر موارد ذکر شده، می‌توان بیان کرد که یک تابع، روی مجموعه‌های مشخصی عمل می‌کند. در ادامه برخی از این مجموعه‌ها را مورد مطالعه قرار می‌دهیم.

به عنوان مثال اول، مجموعه تمام اعداد زوج (مثبت و منفی) را می‌توان با استفاده از مجموعه اعداد زیر نمایش داد.

مشابه مثال بالا می‌توان مجموعه اعداد صحیح فرد را نیز به شکل زیر نمایش داد.

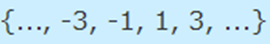
در ادامه مجموعه‌ای شامل تمام اعداد اول را مورد بررسی قرار می‌دهیم. توجه کنید که عدد اول، یک عدد طبیعی بزرگتر از یک است که به هیچ عددی به غیر از یک و خود آن عدد، بخش پذیر نیست. مجموعه این اعداد در رابطه زیر نشان داده شده است.

فیلم‌های آموزشی مرتبط

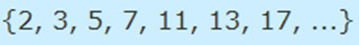
علاوه بر موارد ذکر شده، مجموعه‌ها را می‌توان به اعداد طبیعی، صحیح و گویا نیز محدود کرد. به غیر از مجموعه‌های کلی که در بالا اشاره شد، امکان دارد مجموعه‌های دلخواهی نیز در توابع به عنوان ورودی یا خروجی تعریف شوند. برای مثال ممکن است ورودی یک تابع تنها شامل اعداد مثبت کوچکتر از ۱۰ و مضرب ۳ باشد. این مجموعه دلخواه را به شکل زیر نمایش می‌دهند.

به صورت کلی می‌توان بیان کرد که یک تابع، هرکدام از اعضای یک مجموعه را دقیقا به یکی از اعضای مجموعه دیگر مرتبط می‌کند. توجه کنید که ممکن است دو مقدار از مجموعه اول (دامنه) به یک مقدار از مجموعه دوم (برد) منتقل شوند.

نکته مهم دیگر این است که اگر یک مقدار از مجموعه اول (دامنه) به دو مقدار از مجموعه دوم (برد)، مرتبط شود، با تعرف تابع در تضاد است و این عملگر را نمی‌توان تابع نامید. تعریف تابع و مجموعه دامنه و برد در شکل زیر به خوبی نشان داده شده است.

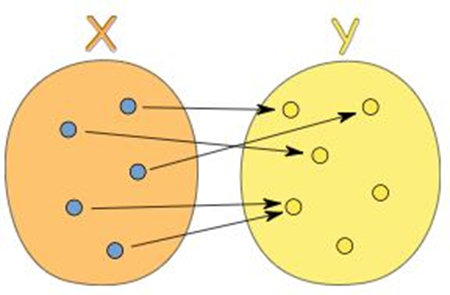
دامنه و برد چیست؟

دامنه یک تابع، مجموعه‌ای است که به عنوان ورودی تابع در نظر گرفته می‌شود و برد تابع، مجموعه‌ای است که تمامی خروجی‌های تابع را در بر می‌گیرد.

مجموعه دیگری نیز تحت عنوان هم‌دامنه در تعریف تابع حضور دارد. هم‌دامنه شامل مجموعه‌ای از اعداد است که خروجی تابع می‌تواند جزئی از آن‌ها باشد. هم‌دامنه را دامنه مشترک نیز می‌نامند. برای مشخص شدن مفهوم این تعاریف به مثال زیر توجه کنید.

مثال

تابعی با رابطه زیر را در نظر بگیرید.

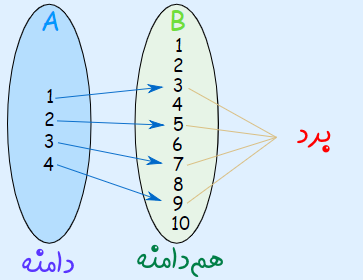
این تابع مانند شکل زیر بین مجموعه‌های A و B عمل می‌کند و هر عضو مجموعه A را به یک عضو مجموعه B مرتبط می‌سازد.

شکل ۴: مفهوم دامنه، برد و هم‌دامنه

بنابراین مجموعه A، دامنه تابع را نمایش می‌دهد و مجموعه B، هم‌دامنه را مشخص می‌کند. توجه کنید که هم‌دامنه را معمولا صورت مسئله تعیین می‌کند و برد، زیر مجموعه‌ای از این هم‌دامنه است.

در این مثال، برد تابع، مجموعه‌ای است که اعداد 3، 5، 7 و 9 را شامل می‌شود. برد این تابع زیر مجموعه‌ای از هم‌دامنه (مجموعه B) است. این سه مجموعه یعنی دامنه، هم‌دامنه و برد را می‌توان به کمک مجموعه‌های زیر هم نمایش داد.

اجزای مختلف یک تابع

در تعریف تابع، دامنه و برد نشان دادیم که آنچه که از تابع بیرون می‌آید (برد تابع) وابستگی مستقیم به ورودی تابع (دامنه تابع) دارد. بنابراین می‌توان بیان کرد که یکی از مهم‌ترین بخش‌های تابع، دامنه آن است و تغییر دامنه باعث تغییر خروجی تابع و ویژگی‌های مختلف آن تابع می‌شود.

برای مشخص شدن مفهوم این قضیه به مثال زیر توجه کنید.

مثال

تابع ساده‌ای را که رابطه آن به فرم f(x)=x2

است را در نظر بگیرید. دامنه این تابع یعنی آنچه به عنوان ورودی به تابع داده می‌شود را می‌توانیم مجموعه‌ای شامل اعداد طبیعی به فرم {1,2,3,...}

تعریف کنیم. با استفاده از این دامنه و رابطه تابع، برد تابع به فرم مجموعه زیر در می‌آید.

{1,4,9,...}

این تابع با استفاده از دامنه و بردی که در بالا تعریف شد، به صورت زیر مشخص می‌شود.

شکل 5: مفهوم دامنه و برد تابع

حال تابع دیگری که رابطه مشابهی با تابع قبلی دارد را در نظر بگیرید. ابن تابع را با حرف g و با استفاده از رابطه g(x)=x2

می‌توان مشخص کرد. دامنه این تابع را به صورت مجموعه تمام اعداد صحیح به فرم زیر در نظر بگیرید.

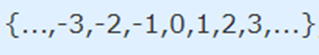
در این شرایط، برد تابع به شکل زیر در می‌آید.

توجه کنید که برد تابع جدید نسبت به حالت قبل یک عدد صفر (0) بیشتر دارد. این تابع، دامنه و برد آن را می‌توان به شکل زیر نمایش داد.

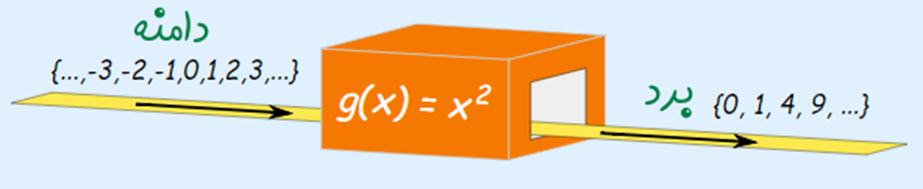
شکل 6: مفهوم دامنه و برد تابع

همانطور که مشاهده می‌شود، هر دو تابع مجذور ورودی را به عنوان خروجی تحویل می‌دهند ولی از آنجایی که این دو تابع ورودی و دامنه متفاوتی دارند، خروجی و برد آن‌ها نیز متفاوت خواهد بود.

توجه کنید که خواص این دو تابع نیز متفاوت است. در حالت اول، تابع f، به صورت یک به یک است و به ازای هر ورودی یک خروجی را تولید می‌کند. این در حالی است که تابع g یک به یک نیست و به ازای دو ورودی مختلف، یک جواب یکسان را تولید می‌کند. این موضوع در دو رابطه زیر نشان داده شده است.

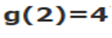بنابراین با توجه به مثال و توضیحات بالا، می‌توان نتیجه گرفت که یکی از بخش‌های اساسی تابع، دامنه آن است. انواع مختلف دامنه می‌تواند ویژگی‌های گوناگون تابع را تحت تاثیر خود قرار دهد. (سایت فرادرس، مقاله دامنه و برد تابع)

تعریف تابع و نگاشت در ریاضیات

به طور شهودی، می‌توان تابع را یک فرآیند یا «عملگر دو دویی» (Binary Operation) در نظر گرفت که به واسطه آن هر عنصری از یک مجموعه به یک عنصر به مجموعه دیگر مرتبط می‌شود. البته نحوه ارتباط در اینجا دارای شرایطی است که در ادامه به آن خواهیم پرداخت.

به طور رسمی تابع f از مجموعه X به مجموعه Y به صورت یک مجموعه است که شامل زوج‌های مرتبی مثل (x,y) بوده که عنصر اول آن از مجموعه X گرفته شده و مولفه دوم آن نیز متعلق به مجموعه Y است. در این بین شرطی وجود دارد که طی آن هر عنصری از X نباید بیش از یک بار در تابع یا مجموعه زوج‌های مرتب، به کار رفته باشد. به بیان دیگر نباید به ازاء‌ یک مقدار از مجموعه X دو مقدار در تابع یا مجموعه Y پیدا شود.

نکته: اگر چنین اتفاقی بیافتد، مجموعه زوج‌های مرتب را یک «رابطه» (Relation)‌ می‌نامند. پس هر تابع یک رابطه است ولی هر رابطه، یک تابع نیست.

نگاشت در ریاضیات

اغلب هر تابع را یک «نگاشت» (Map) در نظر می‌گیرند ولی بعضی ریاضیدانان، برای مفهوم نگاشت و تابع، تمایز قائل می‌شوند. برای مثال «سرژ لانگ» (Serge Lang)، ریاضیدان آمریکایی-فرانسوی، تابع را برای نگاشت‌هایی که هم‌دامنه آن زیرمجموعه‌ای از اعداد حقیقی یا مختلط است به کار می‌برد و معتقد است که نگاشت حالت کلی‌تری از تابع را شامل می‌شود.

از طرفی، اغلب منظور از نگاشت همان «هم‌ریختی» (Homomorphism) است. مثلا برای نشان دادن یک گروه هم‌ریخت از G به H از اصطلاح نگاشت خطی یا نگاشت از G به H استفاده می‌کنند. گاهی هم زمانی یک تابع را نگاشت می‌نامند که هم‌دامنه آن دقیقا منطبق با مجموعه مقادیر تابع باشد. به H از اصطلاح نگاشت خطی یا نگاشت از G به H استفاده می‌کنند. گاهی هم زمانی یک تابع را نگاشت می‌نامند که هم‌دامنه آن دقیقا منطبق با مجموعه مقادیر تابع باشد.(سایت فرادرس، مقاله تابع حقیقی و نگاشت در ریاضیات)

[9] یک معقول منفصل نه مثال منفصل