فصل نهم : ثابت های ریاضی
یکی از مهم ترین مثال ها برای انتقال به اوسعیت نفس الامر از وجود ثابت های ریاضی هستند. هر چند مثال بی نهایت عدد اول بالفعل مثال خوبی است اما انتقال به مقصود غموض خاص خود را دارد به خلاف ثابت های ریاضی که یک عدد ثابت بیش نیستند. آیا ثابت های ریاضی را ذهن ما فرض گرفته است یا ما آنها را درک کرده ایم؟ برای روشن تر شدنمسالهیکی از این ثابت ها را پی گیری می کنیم.
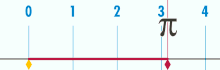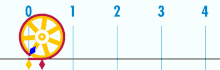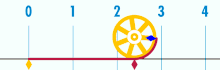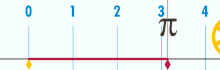
یکی از معروف ترین ثابت های ریاضی عدد پی (π) است. مراد از عدد پی نسبت محیط دایره به قطر آن است، یعنی اگر محیط دایره ای را باز کنیم چند برابر قطر همان دایره است؟ عددی که این نسبت را بیان می کند را عدد پی می گوییم که حرف اول دایره در لغت یونانی بوده و تاریخچهیانبوهی دارد، از اشتباه بابل و مصر و محاسبهیارشمیدس و کشف فرمول محاسبهیآن توسط غیاث الدین جمشید کاشانی تا تعیین جوایزی برای کشف رقم بعدی آن در عصر حاضر.
در اولین گام برای محاسبهیعدد پی به عددی بین 14/3 و 15/3 می رسیم، اما با محاسبهیدقیق تر به عددی بین 141/3 و 142/3 خواهیم رسید. پس رقم بعدی پشت اعشار «1» خواهد بود. در مرحلهیبعد به عددی بین 1415/3 و 1416/3 می رسیم پس رقم بعدی پشت اعشار «5» است. حال سوال این است که دو رقم آخر یعنی «1» و «5» که در 1415/3 دیده می شود قبل از محاسبه معین بودند یا با محاسبهیما معین شدند؟ یعنی آیا ممکن بود هر عددی به جای «1» و «5» باشد و صرفا با محاسبهیما «1» و «5» به دست آمد یا اینکه جز «1» و «5» ممکن نبود عدد دیگری در این رتبه قرار گیرد؟
وقتی که معلوم شد ارقام این ثابت ریاضی که تا بی نهایت ادامه خواهند داشت ثبوت و تقرر بالفعل داشته و نفس الامریت دارند سوال بعدی این است که ظرف ثبوت و تقرر این ارقام کجاست؟ یعنی این بی نهایت رقم بالفعل که بین 14/3 و 15/3 قرار دارند و با فرمول مشخص پیش می روند آیا موجودند یا معدوم؟ آیا عدد پی در دار وجود خارجی است در حالی که عدد پی به عنوان یک عدد «نوع براسه» می باشد و استواء نسبت به وجود و عدم دارد؟ بنابراین لوح تحقق ثابت های ریاضی نظیر عدد پی نمی تواند دار کن ایجادی و ظرف وجود و عدم مقابلی باشد در عین حال می بینیم که عدد پی تقرر و تحقق نفس الامری داشته و به ذهن انسان و محاسبات او وابسته نیست و انسان این حقائق عالم ریاضی را کشف می کند نه اینکه بسازد.

بدون نظر