ج) تبیین نظریه کانتور
دسته بندی کانتور
«بهشت کانتور، بحث راجع به مجموعه های بی نهایت ها و دسته بندی مراتبشان و اعداد ترانسفینی است.
۱. «الف صفر»: مجموعه اعداد طبیعی و...
ایشان مجموعه ها و بی نهایت بودنشان را رده بندی کرده است به همان حرف الفبای عبری[1]، اولین قوه بی نهایت را که اعداد طبیعی هستند اسمش را گذاشته است: «الف صفر».
[ در این کتابهای منطق ریاضی میگویند بینهایتِ اُمگا[2]. اُمگا، آخرین حرف است[3]. یعنی پایینترین بینهایت. اولین بینهایتی که از نظر قوت بینهایتی از همه کمتر است، همان الف صفر است. اینها اعداد بینهایت ها است. یعنی همانطوری که عدد یک و دو داریم، بینهایتها هم درجه بندی دارد. پایینترین بینهایت، الف صفر است که همان بینهایت امگا است[4].]
«الف صفر»، کاردینالش یک کاردینالی ست که اولین درجه ی بی نهایت است.الف صفر، در اعداد ترانفسینی شروع کار است بعد هم اثبات می کند که به برهان قطری کانتور[5] معروف است، برهان خیلی خوبی است.آتئیست ها هم از این برهان برای مقاصد پوچ خودشان استفاده می کنند. در مقاله باخدایی گام به گام عرض کردم. هم استدلال آن ها را آوردم و هم عرض کرده ام که ربطی به مقصود آن ها ندارد[6].
علی ای حال با برهان قطری -در همین کتاب تاریخ ریاضیات هم هست- چه چیزی را ثابت کرده است؟ یک چیز عجیب؛ می گوید:شما بین دو و سه در مجموعه اعداد طبیعی، عددی دیگر پیدا نمی کنید. بینش چیزی نیست.اما هر دو عدد گویا بینش دوباره بی نهایت عدد گویا پیدا می کنید.این چیز کمی است؟! چه قدر گسترده می شود. در عین حال همین آقای کانتور در برهان خودش اثبات کرده که توان بی نهایتی مجموعه اعداد گویا با این فشردگی با توان بی نهایتی مجموعه اعداد طبیعی که می شمریم برابر است. لذا می گوید هر دو شمارا هستند شمارا یعنی تناظر یک به یک دارند.تناظر یک به یک در بی نهایت ها.
۲. «الف یک»: مجموعه اعداد حقیقی
اما وقتی می رسد به مجموعه اعداد حقیقی می گوید نه دیگر.توان بی نهایتی مجموعه اعداد حقیقی که اعداد گنگ هم در آن هست، بیش از «الف صفر» است لذا اسمش را گذاشته است: «الف یک».«الف یک» می شود مجموعه اعداد حقیقی که این همه گستردگی و این همه مباحث برایش مطرح شده است.می گویند: مجموعه اعداد حقیقی، به اندازه کافی فشرده است؛
یعنی غیر از این که هر دو نقطه اش بینش بی نهایت نقطه و عدد هست، هیچ جای خالی هم بینش نمی توانید پیدا کنید و لذا ناشماراست. کانتور برهان خلف اقامه می کند که «الف یک» مجموعه اعداد حقیقی ناشماراست. یعنی دیگر با اعداد طبیعی هم قوه نیستند. [یعنی خطی که اعداد حقیقی است، اعداد طبیعی و شمارشی نمیتواند آنها را بشمارد[7]]
از همین برهان خلف کانتور، یک مبنای فلسفه ریاضی پیدا شده است[8].
مبانی سه گانه در فلسفه ریاضیات
سه تا مبنا هست در منطق ریاضی و فلسفه ریاضی که زیاد از آن اسم می برند:
۱. صورت گرایی[9] فرمالیسم،
۲. منطق گرایی [10]Logicism،
۳. یکی هم شهودگرایی مال براور[11].
شهودگرایی همین است. می گوید: برهان خلف کانتور را در اثبات «الف یک»، مجموعه اعداد حقیقی قبول ندارم.باید حتماً بسازیم تا اثبات کنیم. به صرف برهان خلف اثبات نمی شود.این ها هم بحث های خوبی است که در قرن بیستم انجام شده است[12].»
[1] الفبای عبری از ۲۲ حرف تشکیل شدهاست. صداهای زیر شیوهٔ تلفظ حروف عبری هستند
آلِف א -- بِت ב – وِت ב -- گیمِل ג – دالِت ד – هِ ה – واو ו – زایین ז – خِت ח – تِت ט – یُد י – کاف כ – خاف כ -- خافْ سُفیت ך -- لامِد ל – مِم מ – مِمْ سُفیت ם -- نون נ – نون سُفیت ן -- سامِخ ס – عایین ע – پِ פ -- فِ פ -- فِ سُفیت ף -- تْسادی צ – تْسادی سُفیت ץ -- کُف ק – رِش ר – شین ש – سین ש -- تاو ת
[2] Aleph-omega is
ℵω = sup{ ℵn | n ∈ ω } = sup{ ℵn | n ∈ {0, 1, 2, ...} }
where the smallest infinite ordinal is denoted as ω. That is, the cardinal number ℵω is the least upper bound of
{ ℵn | n ∈ {0, 1, 2, ...} }.
Notably, ℵω is the first uncountable cardinal number that can be demonstrated within Zermelo–Fraenkel set theory not to be equal to the cardinality of the set of all real numbers 2ℵ0: For any natural number n ≥ 1, we can consistently assume that 2ℵ0 = ℵn, and moreover it is possible to assume that 2ℵ0 is as least as large as any cardinal number we like. The main restriction ZFC puts on the value of 2ℵ0 is that it cannot equal certain special cardinals with cofinality ℵ0. An uncountably infinite cardinal κ having cofinality ℵ0 means that there is a (countable-length) sequence κ0 ≤ κ1 ≤ κ2 ≤ ... of cardinals κi < κ whose limit (i.e. its least upper bound) is κ (see Easton's theorem). As per the definition above, ℵω is the limit of a countable-length sequence of smaller cardinals.(Wikipedia)
عدد ترتیبی مجموعه اعداد طبیعی N ، با رابطه کوچکتر یا مساوی معمولی، را معمولاً با حرف یونانی امگا ωنشان میدهند؛ یعنی:
ω =ord(1,2,3,…) (آشنایی با نظریّه مجموعهها و کاربردهای آن، ص ۱۶۹)
بررسی اعداد اردينال به تعاريف مقدمات زيادینياز دارد وما آنها را به صورت فشرده ای اينجا بيان می كنيم :
در تمام اين بحث صفر را هم عضوی از اعداد طبيعی در نظر ميگيريم.
مجموعه خوش ترتيب: يك مجموعه همرا با يك رابطه ترتيب را خوشترتيب گوييم هرگاه هر زير مجموعه آن دارای عضو اقل (كوچكترين عضو ) باشد. مثل مجموعه اعداد طبيعي.
دو مجموعه مرتب كه تنها برچسب گذاری اعضايشان با هم تفاوت دارد را يكريخت ترتيبی (order isomorphic) گوييم، به اين معنا كه " عضوی از مجموعه اول از عضوی ديگردر اين مجموعه كوچكتر باشد اگر وتنها اگر همتای آن عضوی از مجموعه دوم پيدا شود كه از عضوی از آن مجموعه كوچكتر است" ، كه به اين تناظر يك به يك يكريختی ترتيبی (order isomorphism) گويند.مثلا مجموعه های خوش ترتيب {3و2و1}و {16و15و14}يكريخت ترتيبی هستند . يعنی اولين عضو در يك مجموعه برچسب 1 و در مجموعه ديگر برچسب 14 دارد وبه همين ترتيب دومين و سومين عضو .
اكنون می توان با اين يكريختی رده های هم ارزی تعريف كرد.كه در هر رده همه مجموعه های يكريخت ترتيبی قرار دارند.
اعداد اردينال
اولين تعريف عدد اردينال :يك عدد اردينال مجموعه خوشترتيبی است مثل a كه هر عضو آن مثل x برابر با مجموعه عناصری از a باشد كه از x كوچكترند.
اعداد اردينال در رياضيات به زبانهای مختلفی تعريف شده اند،اكنون ما به بررسی مختصر ماهيت آن می پردازيم.
به زبان خيلی ساده اعداد اردينال رده های هم ارزی مجموعه های خوشترتيب را برچسب گذاری می كند.يا هر عدد اردينال يك نماينده از دسته هم ارزی مجموعه های خوشترتيب را مشخص می كند.
در حالت خيلی ساده مجموعه اعداد طبيعی را در نظر بگيريد ،زير مجموعه های زير را در نظر بگيريد
{},{0},{0,1},{0,1,2},.......
(كه اين زير مجموعه ها در واقع نماينده مجموعه های مرتب متناهی هستند)
برای اين زير مجموعه ها دو نوع برچسب گذاری می توانيم انجام دهيم
1. برچسب كاردينالی كه به هر مجموعه تعداد اعضا (بحث بر روی اندازه مجموعه(size) ) را نسبت می دهدمثلا برچسب مجموعه {1و0} عدد 2 خواهد بود.
2. برچسب اردينالی كه به هر مجموعه برچسب ترتيب آن مجموعه(بحث روی موقعيت اعضا position) را می زند ، توجه داريم كه اين مجموعه ها نماينده رده های ترتيبی مجموعه های مرتب متناهی هستند مثلا مجموعه{2و1و0} نماينده همه مجموعه های ترتيبی 3 عضوی است.البته در حالت متناهی اين دو نوع برچسب گذاری يكسان هستند(چون هر دو مجموعه ترتيبی متناهی با تعداد اعضای يكسان يكريخت ترتيبی هستند). اما در حالت نا متناهی كاملا متفاوتند .
خب پس تا اينجا اعداد اردينال متناهی به صورت زير تعريف شده اند(كه در اين حالت همان اعداد طبيعی هستند)
0,1,2,3,....
كه برچسب مجموعه های خوشترتيب و متناهی زير هستند:
{ } ,{0} ,{0,1} ,{0,1,2},.....
به طور مثال عدد اردينال 26 يعنی مجموعه خوشترتيب {25و......و1و0}
پس برای مجموعه های مرتب متناهی كه اعداد اردينال (كه گاهی برای سادگی فقط می گويند اردينال) چيز جديدی نيستند.اما در حالت نامتناهی وضع به كلی فرق ميكند به هر مجموعه نامتناهی تنها يك برچسب اندازه (كاردينال )دارد اما يك مجموعه خوش ترتيب نامتناهی می تواند چند رده خوشترتيب غير يكريخت داشته باشد.
در واقع گسترش و توسيع برچسب اندازه برای مجموعه های نامتناهی منجر به تعريف كاردينال يك مجموعه و گسترش و توسيع برچسب ترتيب مجموعه های نامتناهی منجر به تعريف اردينال يك مجموعه می شود.
مجموعه همه اعدادطبيعی {...و4و3و2و1و0} كه يك مجموعه نامتناهی و خوشترتيب است اولين عدد اردينال نامتناهی را مشخص ميكند كه آنرا با ω نمايش ميدهيم .
اعداد اردينال را ميتوان با هم جمع، ضرب يا به توان رساند، اما جمع و ضرب آنه لزوما خاصيت جابجايی ندارند يعنی مثلا ω =1+ω ولی اين اكيدا كوچكتر از ω+1 هست و ω برابر2ضربدر هستش.اما اكيدا كوچكترازω.2 هست (نحوه جمع و ضرب اين اعداد را می توانيد در مراجع مشاهده كنيد).وداريم
ω={0,1,2, ......}
ω+1={0,1,2,....,ω
.....
كه عدداصلی همه مجموعه های اخير همان عدد اصلی اعداد طبيعی (الف نات)هستش و مجموعه همه اعداد اردينال شمارا را با
ω1نشان می دهيم وعدد اصلی آن الف يك هست.و اين اولين عدد اردينال ناشماراست.
اكنون می توان اين مجموعه ها رو ادامه داد ومجموعه خوشترتيب اعداد اردينال مجموعه زير خواهد شد
مثلا ω يعنی مجموعه همه اردينالهای متناهی و 3 يعنی برچسب همه3 عضوی های خوشترتيب والی آخر
بحث اردينالها يك بحث فوق العاده پركاردر نظريه مجموعه هاست كه تعريف های آن در رياضيات با ابزارهايی مثل توپولوژی ، نيز آمده است و من هرچه مينويسم باز هم ميبينم قسمتهای زيادی برای گفتن مانده برای مطالعه بيشتر به آدرسهای كه درپايان مطلب خواهم گذاشت می توانيد مراجعه كنيد.
در نهايت تعريف جان فون نويمان رياضيدان معاصر را از عدد اردينال ذكر ميكنيم كه می توانيد انطباق تعاريف بالا از عدد اردينال را با تعريف فون نويمان در مثال زير تعريف ببينيد.(زندگی با ریاضیات، مقاله آشنایی با اعداد اوردینال)
در این زمینه همچنین: Why is ω the smallest ∞?
باید توجه داشت که کانتور علاوهبر بیان مجموعه اعداد ترانفسینی، از مفهومی با عنوان نامتناهی مطلق یا absolute infinite با نماد حرف بزرگ امگا (Ω)یاد میکند که بسط و توسعه مفهوم نامتناهی است و با مجموعه بینهایت امگا متفاوت است.( (absolute infinite
[3] اومگا (بزرگ: Ω، کوچک: ω; یونانی Ωμέγα) بیست و چهارمین حرف الفبای یونانی است. و در دستگاه شمارش یونانی مقدار ۸۰۰ را دارد. نام این حرف به معنی اوی بزرگ است (ō مگا، مگا به معنی بزرگ است)، که در مقابل امیکرون است "little O" (به معنای اوی کوچک).
[4] جلسه شرح توحید صدوق، تاریخ 26/9/1398.
[5] در نظریه مجموعهها، استدلال قطری کانتور در سال ۱۸۹۱ توسط گئورگ کانتور به عنوان یک اثبات ریاضی ارائه گردید و نشان داد مجموعههای نامتناهی وجود دارند که اعضای آنها در تناظر یک به یک با مجموعه اعداد طبیعی نیستند. چنین مجموعههایی را «مجموعه ناشمارا» مینامند.
مجموعه غیرقابل شمارش
کانتور، در مقالهی خود در سال ۱۸۹۱، مجموعه T را مطالعه کرد که شامل همه دنبالههای رقمهای دودویی (یعنی هر رقم صفر یا یک) باشد. او با اثباتی ساختی از قضیه زیر شروع میکند:
اگر s1, s2, … , sn شامل تمامی شمارشهای ممکن از T باشد، آنگاه همواره عضوی از T وجود خواهد داشت که در بین s1,S2,... نخواهد بود.
برای اثبات این، مجموعههایی از T را به شکل زیر انتخاب مینماییم:
s1 = (۰, ۰, ۰, ۰, ۰, ۰, ۰, ...)
s2 = (۱, ۱, ۱, ۱, ۱, ۱, ۱, ...)
s3 = (۰, ۱, ۰, ۱, ۰, ۱, ۰, ...)
s4 = (۱, ۰, ۱, ۰, ۱, ۰, ۱, ...)
s5 = (۱, ۱, ۰, ۱, ۰, ۱, ۱, ...)
s6 = (۰, ۰, ۱, ۱, ۰, ۱, ۱, ...)
s7 = (۱, ۰, ۰, ۰, ۱, ۰, ۰, ...)
...
او ساختار توالی s را با انتخاب مکمل اولین رقم در s1 انتخاب نمود (جایگزینی صفر به جای یک و برعکس)، برای انتخاب دومین رقم S به سراغ رقم دوم در s2 رفت و مکمل آن را انتخاب نمود و به همین ترتیب ادامه داد. در مثال فوق به نتایج زیر میرسیم:
s1 = (۰, ۰, ۰, ۰, ۰, ۰, ۰, ...)
s2 = (۱, ۱, ۱, ۱, ۱, ۱, ۱, ...)
s3 = (۰, ۱, ۰, ۱, ۰, ۱, ۰, ...)
s4 = (۱, ۰, ۱, ۰, ۱, ۰, ۱, ...)
s5 = (۱, ۱, ۰, ۱, ۰, ۱, ۱, ...)
s6 = (۰, ۰, ۱, ۱, ۰, ۱, ۱, ...)
s7 = (۱, ۰, ۰, ۰, ۱, ۰, ۰, ...)
...
s = (۱, ۰, ۱, ۱, ۱, ۰, ۱, ...)
با ساخت s به روش فوق به مجموعهای میرسیم که با تمامی مجموعههای بالا متفاوت است زیرا عنصر n ام آن با عنصر n ام تمام مجموعههای بالا تفاوت دارد.
بر اساس این قضیه کانتور با استفاده از یک اثبات با تناقض نشان میدهد که:
مجموعه T غیرقابل شمارش است.
او برای اثبات تناقض در ابتدا فرض میکند T شمارا است. پس همه عناصر آن به شکل s1,s2,...sn قابل نمایش هستند. با اعمال قضیه قبلی به این شمارشها به توالی s میرسیم که در شمارشها موجود نیست. اما s عنصری از T بود و بنابراین باید در شمارشها باشد. این تضاد فرض اصلی را زیر سؤال میبرد بنابراین T غیرقابل شمارش است.(سایت ویکی پدیا) همچنین ملاحظه کنید: Universality and the Liar: An Essay on Truth and the Diagonal Argument
تصویر روشنتری از این برهان را در اینجا میتوانید مشاهده کنید.
در زمینه کاربرد برهان قطری در مباحث حکمت نیز مطالعه مقاله «بررسی اهمیت فلسفی برهان قطری کانتور» سودمند است.
[6] این بخش از مقاله با خدایی گام به گام را در فصل دوم این نوشتار ملاحظه خواهید کرد.
[7] جلسه شرح توحید صدوق، تاریخ 26/9/1398
[8] سه فلسفه اصلی یا مکتب تفکر در رابطه با مبانی ریاضیات پیدا شده است به اصطلاح مكتب منطق گرا، مكتب شهودگرا و مكتب صوری گرا .طبیعی است که هر فلسفه نوین مبانی ریاضیات باید ، به نحوی، با بحران کنونی درمیانی ریاضیات مقابله کند . در بخش آتی به طور مختصر این سه مکتب فکری را مورد بررسی قرار داده و متذکر خواهیم شد که چگونه هر یک از اینها راهی برای مواجهه با تعارضهای نظریه عام مجموعه ها در پیش پا می گذارد. (تاریخ ریاضیات، ج ۲، ص ۳۲۰)
[9] تز صوری گرا این است که ریاضیات با دستگاه های نمادی صوری سر و کار دارد. در واقع ریاضیات مجموعه ای از آن مباحث مجرد تلقی می شود که در آن اصطلاحات صرفا نمادهایی هستند و احکام قواعدی متضمن این نمادها. پایه غائی ریاضیات در منطق قرار ندارد و بلکه تنها در مجموعه ای نشانه ها و نمادهای پیش منطقی و در مجموعه ای از اعمال با این نشانه ها واقع است. چون از این دیدگاه، ریاضیات عاری از محتوای ملموس و تنها شامل عناصر نمادی آرمانی است، برقراری سازگاری شاخه های مختلف ریاضیات قسمت مهم و لازمی از برنامه صوری گرایی می شود. بدون همراهی چنین برهان سازگاری، تمام مبحث اساس بی معنی خواهد شد. در تز صوری گرایی اصل موضوعی ریاضیات در بیشترین حد دنبال می شود.
مکتب صوری گرایی توسط داوید هیلبرت بعد از اتمام کارش در بررسی اصل موضوعی هندسه تاسیس شد. در مبانی هندسه اش 1899 هیلبرت روش ریاضی را از قالب مبحث اصل موضوعیهای مادی اقلیدس به قالب دقیق تر مبحث اصل موضوعیهای صوری کنونی در آورده بود. دیدگاه صوری گرا بعدا برای مقابله با بحران ناشی از پارادوکسهای نظریه مجموعه ها و به مبارزه طلبیدن ریاضیات کلاسیک به دلیل انتقادهای شهودگرایانه، به وسیله هیلبرت ایجاد شد. گرچه هیلبرت پیش از سال 1904 اصطلاحات صوری گرایانه را به کار برده بود تا بعد از سال 1920 وی و همکارانش برنیس، آکرمان، فون نویمان، و دیگران کار جدی را درباره آنچه امروزه برنامه صوری گرا نامیده می شود آغاز نکردند.
توفیق یا شکست برنامه هیلبرت برای نجات ریاضیات کلاسیک در گرو حل مسئله سازگاری است. بری بودن از تناقض تنها به کمک برهان های ناسازگاری تضمین می شود و برهان های ناسازگاری قدیمی تر مبتنی بر تعابیر و مدل هایی است که مسئله سازگاری را از یک حوزه ریاضیات به حوزه دیگر منتقل می کند. به عبارت دیگر یک برهان سازگاری به روش مدلها صرفا برهانی نسبی است. بدین جهت هیلبرت روش مستقیم جدیدی برای مسئله سازگاری تدبیر کرد. بسیار شبیه به اثبات انچه وضعیت هایی خاص در یک بازی بنابر قواعد آن نمی توانند در بازی پیش آیند هیلبرت امید آن را داشت تا به کمک مجموعه مناسبی ار قواعد عمل برای به دست آوردن فرمول های قابل قبول از نمادهای اساسی ثابت کند که فرمول متناقضی هرگز پیش نمی آید. با نمادهای منطقی یک فرمول متناقض فرمولی که از نوع " F و نه F " است که در آن F فرمول پذیرفته شده ای از دستگاه است. اگر بتوان نشان داد که چنین فرمول متناقضی ممکن نیست آنگاه سازگاری دستگاه ثابت شده است.
بسط افکار فوق برای آزمون مستقیم سازگاری دری ریاضیات توسط هیلبرت، نظریه برهان نامیده شد. برای دستگاه های مقدماتی معینی براهین سازگاری فراهم شدند که آنچه را هیلبرت میل به انجام آن برای همه ریاضیات کلاسیک داشت نشان می دهد ولی در کل مسئله ناسازگاری برای دستگاه بدون چاره ماند.
در حقیقت برنامه هیلبرت حداقل به شکلی که در اصل در ذهن او بود ظاهرا محکوم به شکست بود این حقیقت توسط کورت گودل در سال 1931 عملا قبل از انتشار مبانی ریاضی، آشکار شد. گودل به کمک روش های بی ایراد و قابل قبول برای پیروان هر یک از سه مکتب اصلی فلسفه ریاضیات نشان داد که برای دستگاه قیاسی که به حد کافی صوری شده باشد نظیر دستگاه هیلبرت برای همه ریاضیات کلاسیک اثبات سازگاری دستگاه به کمک روش های متعلق به خود آن دستگاه میسر نیست. این قضیه قابل توجه پیامد قضیه اساسی تری داشت گول ناکامل بودن دستگاه هیلبرت را ثابت کرد یعنی وی وجود مسائل "تصمیم ناپذیر" را در داخل دستگاه که سازگاری دستگاه از آن جمله است نشان داد. این قضایا نشان می دهند که دستگاه های ریاضی که برای استخراج ریاضیات مناسب شناخته شده اند قابل اطمینان نیستند بدین معنی که سازگاری آنها را نمیتوان با روش های متناهی داخل دستگاه صوری شده اند ثابت کرد و حال آنکه هر دستگاهی که از این لحاظ مطمئن تشخیص داده شده نامناسب است.(مقاله صوری گرایی در ریاضیات استفاده شده از مطالب کتاب تاریخ ریاضیات)
[10] پئانو نظریه ی اعداد طبیعی را اصل موضوعی ساخت و قدم اصلی را برای حسابیدن ریاضیات، یعنی تحویل ریاضیات به حساب، برداشت. وی سه مفهوم اولیه صفر، عدد و تالی را ارائه کرد ( مقصود از عدد، عدد طبیعی و منظور از تالی، عدد بعدی در تربیت طبیعی بود، مثلاً یک تالی صفر است، دو تالی یک است و قس علی هذا). سپس پنج اصل موضوع زیر ( موسوم به اصول پئانو) را وضع کرد:
الف) صفر یک عدد است.
ب) تالی هر عدد، یک عدد است.
ج) صفر تالی هیچ عددی نیست.
د) هیچ دو عدد متفاوتی دارای تالی برابر نیستند.
ه) هر خاصیتی که به صفر و به تالی هر عدد دارای آن خاصیت متعلق، باشد، به همه اعداد متعلق است ( اصل استقرای ریاضی). به این ترتیب می توانیم رشته اعداد طبیعی را با شروع از صفر و گذر از یک عدد مانند n به تالی آن یعنی (s(n در دست داشته باشیم.
جمع به سادگی قابل تعریف است. در واقع به ازای هر m ، عدد 0+mرا برابر m قرار می دهیم و اگر m+n داده شده باشد،(m+s(nرا برابر تالی m+n یعنیs(m+n) تعریف می کنیم. ضرب نیز به طور مشابه تعریف می شود و به دنبال آن می توان همه قضایای حساب ( مقدماتی) را اثبات نمود.
کار پئانو ایرادتی داشت، از جمله این که دستگاه قیاسی وی قابلیت پذیرفتن تعدادی نامتناهی تعبیر را داشت. یک تعبیر این است که صفر را به معنی صد، عدد را به معنای اعداد طبیعی بزرگتر یا مساوی صد و تالی را به معنای معمولی آن می گیریم. در این صورت هر پنج اصل موضوع پئانو، احکام صادقی خواهند بود ( توجه کنید که صد تالی نود و نه نیست زیرا در این الگو نود و نه عدد نیست!).
بر طبق نظر راسل، در دستگاه پئانو چیزی برای تمیز دادن الگوهای متفاوت وجود نداشت. ما می دانیم « صفر» چه باید باشد، به ویژه نمی خواهیم به معنای صد باشد. دستگاهی که در آن صفر به معنای صد است به درد زندگی نمی خورد. می خواهیم اعدادمان چنان باشند که بتوانند برای شمارش اشیای معمولی به کار روند.
در 1884 فرگه به منطقیدن حساب، یعنی تقلیل حساب به منطق ( و با توجه به کار پئانو، در واقع منطقیدن ریاضیات) همت گماشت و اولین مکتب ریاضی را به نام منطق گرایی، که به عقیده ی کواین یک رهیافت افلاطون گرایانه به ریاضیات بود، تأسیس کرد . هدف این مکتب تحویل ریاضیات به منطق بود، یعنی اثبات این که ریاضیات شاخه ای از منطق ( جدید و نه سنتی ) است.
به زعم فرگه عدد چیزی است که مشخصه اعداد است همان طور که انسان مشخصه انسان ها است. یک عدد خاص مانند 3 نمونه ای از عدد است و یک گروه سه نفری نمونه ای از عدد 3 است، و نه عدد. خود عدد 3 چیزی است که بین همه ی گرد آیه های سه عضوی مشترک است. فرگه صفر را گرد آیه ی متشکل از مجموعه ی تهی، 1 را گرد آیه ی متشکل از همه مجموعه های تک عضوی، 2 را گرد آیه متشکل از همه ی مجموعه های دو عضوی و ...تعریف کرد.
با این حال همه ی این ها، توسط راسل دوباره کشف شد. در واقع منطق گرایی در حدود 1910 توسط راسل و وایتهد تنقیح شد. این دو نفر سعی کردند نشان دهند تمام ریاضیات کلاسیک که تا آن زمان شناخته شده بود از نظریه ی مجموعه ها و این نظریه در جای خود از اصول موضوع مذکور در کتاب اصول ریاضیات آن ها مشتق می شود و بالاخره که این اصول موضوع متعلق به منطق هستند.
آن ها در ارائه ی منطق گرایی نظریه ی انواع و اصل تقلیل پذیری را به کار بردند. اما برنامه ی آن ها ناقص بود، زیرا مثلاً این اصل موضوع که مجموعه های نامتناهی وجود دارند یک حکم منطقی ( یعنی حکمی با عمومیت کامل که صدقش در پرتو صورتش باشد نه محتوایش) نبود. در واقع پذیرش این اصل به خاطر آشنایی ما با مجموعه های نامتناهی مانند مجموعه اعداد طبیعی یا مجموعه نقاط فضای سه بعدی بود، یعنی بر مبنای مضمون این اصل، نه صورت آن. همین وضعیت در مورد اصل انتخاب نیز برقرار بود. مشکل دیگر این بود که فرآیند استخراج قضایا از اصول منطق، طویل، پیچده و ملال آور بود و با دید شهودی ما از ریاضیات منطبق نبود. به این ترتیب، منطق گرایی در ارائه قواعد و اصول زیر بنایی ریاضی شکست خورد.(سایت راسخون، مقاله منطق گرایی در ریاضیات)
[11] تز شهودگرا آن است که ریاضیات باید منحصراً به توسط يك عدهم تناهی از روشهای سازنده درباره دنباله اعداد طبیعی که به طور شهودی در نظر گرفته شده اند بنا شود. لذا مطابق این نظر در زیربنای ریاضیات شهود اولیه ای قرار دارد که بدون تردید با حس گذرایی قبل و بعد در وجود ما همراه است و به ما اجازه می دهديك چیز واحد، سپس یکی دیگر سپس یکی دیگر و همینطور تا به طور بی پایان را تصور کنیم. بدین ترتیب دنباله های بی انتها را به دست می آوریم که معروفترین آنها دستگاه اعداد طبیعی است. از این مبنای شهودی دنباله اعداد طبیعی هر شی ریاضی دیگر را باید به يك روال سازنده بنا کرد و در آن تعدادی متناهی از مراحل یا اعمال را به کار برد در تز شهود گرابسط ریاضیات از لحاظ تکوینی تا سر حد امکان دنبال می شود.
مکتب شهودگرا ) به عنوان يك مكتب ( در حدود سال ۱۹۰۸ به توسط ریاضیدان هلندی ل . ا . ى . بر اوثر آغاز شد ولی برخی مفاهیم شهودگرایانه قبلا توسط کسانی چون کرونکر در سالهای (۱۸۸۵) و پوانکاره (۱۹۰۲ - ۱۹۰۶) ابراز شده بود. این مکتب با گذشت زمان تدریجاً تقویت شده، برخی از ریاضیدانان برجسته کنونی را به خود جلب کرده و تأثیر فوق العاده ای در تمام افکار مربوط به مبانی ریاضیات گذاشته است.
برخی از پیامدهای تز شهودگرا جنبه انقلابی دارند. مثلاً پافشاری بر روشهای سازنده به تصوری از وجود در ریاضیات منجر میشود که آن چیزی نیست که همه ریاضیدانان به آن اعتقاد داشته باشند برای شهودگرایان ، هستیی که اثبات وجود آن لازم است باید در تعدادی مراحل متناهی ساختنی باشد کافی نیست که فرض عدم وجود آن هستی منجر به تناقض شود. این بدان معنی است که بسیاری از براهین وجودی زیادی که در ریاضیات کنونی دیده میشوند برای شهودگرایان قابل قبول نیستند.
مورد مهمی از پافشاری شهودگرایان بر روشهای سازنده نظریه مجموعه هاست. از نظر شهودگرايان يك مجموعه را نمی توان به عنوان گردایه ساخته و پرداخته ای تصور کرد بلکه باید آن را به عنوان قانونی تلقی کرد که به کمک آن عناصر مجموعه را بتوان به يك روال قدم به قدم بنا کرد. این مفهوم مجموعه امکان وجود مجموعه های تناقض آمیزی مانند مجموعه همه مجموعه ها » را رد می کند. (تاریخ ریاضیات، ج ۲، ص ۳۲۴)
در این زمینه همچنین مراجعه کنید به سایت بریتاینکا: مقاله Logicism, intuitionism, and formalism
[12] جلسه سوم تاریخ اجمالی ریاضیات؛ بحرانها و مسائل

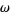 ,
, 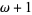
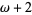
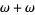
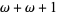 ,....
,....
بدون نظر