الف) اعداد و مجموعه های آن

الف) اعداد و مجموعه های آن

۱. مجموعه اعداد طبیعی

[1]«از مطالب خیلی ساده، این است که مثلاً در مجموعه اعداد طبیعی[2] که از یک شروع می‌شود و تا بی‌نهایت می‌رود. بین دو عضو از این مجموعه، دیگر نمی‌توانید چیزی از اعداد طبیعی پیدا کنید. وقتی سر و کارتان با اعداد طبیعی است، بین دو و سه، چه عددی است؟ هیچی. بعد از دو، سه است و بین آن‌ها چیزی نیست. همچنین اعداد صحیح مثبت و منفی. تمام اعداد صحیح به این صورت است، یعنی بین دو عضو از یک مجموعه، عضو دیگری نیست.

۲. مجموعه اعداد گویا

اما وقتی سراغ اعداد گویا[3] می‌رویم، تعبیر بسیار مهم و اعجاب‌آوری است؛ وقتی آدم به آن فکر می‌کند واقعاً بهتش می‌گیرد. مجموعه اعداد گویا چیست؟ یعنی آن عددی که از نسبت بین دو عدد حاصل می‌شود. الآن بین یک و دو، عددی نداشتیم، اما می‌گوییم یک دوم؛ یعنی نصف. دو سوم، سه چهارم. یعنی همین فاصله‌ای که بود، دو و یک سوم؛ بین دو و سه دارید عدد پیدا می‌کنید. این‌ها اعداد نسبی می‌شوند. اعدادی که مُنطَق و گویا هستند.

مجموعه اعداد گویا؛ فشرده

چیز عجیب و غریب این است که ریاضی‌دان‌ها می‌گویند: مجموعه اعداد گویا فشرده است[4]. این فشرده یعنی چه؟ خیلی مهم است. فشرده یعنی هر دو عدد گویا در هر کجا پیدا کنید، نه تنها بین آن‌ها فقط یک عدد نیست، بلکه دوباره بی‌نهایت عدد گویا است؛ خیلی است. اگر دو عدد گویا مثلاً یک دوم با یک سوم را با کسرها مدام به هم نزدیک کنید، بی‌نهایت جلو بروید و به جایی برسید که تصورش سخت است، باز بین آن دو عدد گویا، بی‌نهایت عدد گویا است. وقتی فکرش را می‌کنید، این فشردگی یک امر بهت‌آوری است. یعنی دوباره بین هر دو عضو، بی‌نهایت عضو از همان مجموعه هست؛ به این، فشردگی می‌گویند. این درکش ساده است.

مجموعه اعداد گویا؛ شمارا

اما آنچه که ره‌آورد قرن بیستم بود و بهت‌آور است، این است - با برهانی که در فضای ریاضی ثابت شده - که می‌گویند: این مجموعه‌های اعداد گویا که فشرده است، شماراست[5]. شمارا به چه معنا است؟ یعنی تناظر یک به یک[6] دارد با مجموعه اعداد طبیعی. از نظر قوّه‌ی بی‌نهایت، با اعداد طبیعی یکی است[7]. به اصطلاح اعداد ترانسفینی[8]، هر دویش الفْ صفر است.

اعداد طبیعی فشرده نبود؛ بین هر دو عضوش فاصله‌ای نبود. این مجموعه اعداد طبیعی با اعداد گویایی که بین هر دو عضوش، بی‌نهایت عضو است، از نظر زور بی‌نهایت بودن، یکی هستند. از نظر اعداد بی‌نهایت‌ها، هر دو، الف صفر هستند و شمارا. شمارا یعنی تناظر یک به یک دارد با مجموعه اعداد طبیعی.

- الف صفر، به چه معنا است[9]؟

الف صفر، نام عددهای بی‌نهایت‌ها است. عدد ترانسفینی می‌گویند؛ اعداد متعالی. الف صفر، اولین آن‌ها است که همان اعداد طبیعی است و هر مجموعه بی‌نهایتی که با اعداد طبیعی بی‌نهایت اول، تناظر یک به یک داشته باشد، شمارا است؛ می‌توانیم آن را بشماریم و درجه بی‌نهایت بودنش با درجه اعداد طبیعی قوّتش برابر است.

۳. مجموعه اعداد حقیقی

حالا مهم این بود:

مجموعه اعداد حقیقی؛ ناشمارا

مجموعه اعداد حقیقی نا شماراست. یعنی نمی‌توان آن را شمرد؛ تناظر یک به یک ندارند. از اینجا نتیجه می‌گیریم که مجموعه اعداد گویا هرچند فشرده است، اما به اندازه کافی فشرده نیست؛ تعبیری است که دارند. یعنی ولو بین دو عدد باز بی‌نهایت عدد است، اما باز روی محور، نقاطی را پیدا می‌کنیم که گویا نیست و گنگ است. در اعداد غیرگویا، هم اعداد رسم‌پذیر و هم غیررسم‌پذیر هستند، مثل عدد پی[10]  که اصلاً رسم‌پذیر نیست یا  اعداد گنگی که رسم‌پذیر است، مثل رادیکال دو که با خط‌کش و پرگار نشانش می‌دهیم؛ می‌گویند این نقطه را که می‌بینی، این نقطه، عدد گویا نیست. محال است بتوانید آن را به یک عدد گویا بیان کنید، ولی نقطه آن، این است. پس معلوم شد اعداد گویا که این قدر گسترده است، باز بی‌نهایت عدد داریم که در مجموعه اعداد گویا نیست؛ این خیلی مهم است[11].[12]»

[1] نوشته پیش رو، تنظیم و گردآوری مطالبی است که در جلسات مختلف از جمله جلسات  هشتم، یازدهم و سی و دوم فقه هوش مصنوعی و جلسه شرح توحید صدوق  تاریخ 26/9/1398 و جلسه سوم مرور اجمالی تاریخ ریاضیات افاده شده است. علاوه‌بر افادات، از متن مقاله باخدایی گام به گام در فصل دوم و تقریرات شرح این مقاله که در جلسات خارج اصول فقه به تناسب مطرح شده است بهره برده‌ایم.

[2] اعداد طبیعی یا اعداد صحیح مثبت اعدادی هستند که از یک ( ۱ ) شروع می‌شوند و تا بینهایت (عدد n) ادامه دارند. و شامل صفر نمی‌شود (عدد صفر مرز میان اعداد مثبت ومنفی است) و برای شمارش (به‌طور مثال در «شش سکه روی میز است») و برای ترتیب (به‌طور مثال در «این سومین شهر بزرگ در کشور است») به کار می‌روند. در اصطلاح‌شناسی ریاضیات، لغت مورد استفاده برای شمارش اشیاء واقعی «اعداد ترتیبی» است. مجموعهٔ اعداد طبیعی همان مجموعهٔ اعداد صحیح مثبت یعنی {... و۱٬۲٬۳} است. این اعداد شامل اعداد مرکب، اعداد اول و یک است. به بیان ساده، عدد طبیعی، عددی است که در طبیعت وجود دارد و برای شمردن عناصر طبیعی استفاده می‌شوند، برای مثال عدد صفر یا اعداد منفی در طبیعت وجود ندارند و در مجموعه اعداد طبیعی نیستند.(سایت ویکی پدیا)

[3] عدد گویا یا عدد کسری (به انگلیسی: Rational number) در علم ریاضیات، عددی است که می‌تواند به صورت کسر یا ( p / q ) از دو عدد صحیح p و q ( به طوری که p صورت کسر و q مخرج کسر باشد.) بیان شود. به عبارت دیگر، اعداد گویا کسرهایی هستند که از تقسیم عدد صحیح بر عدد صحیح دیگر (به جز صفر) پدید آمده باشد.  از آن‌جایی که q می‌تواند برابر با عدد یک باشد؛ پس تمامی اعداد صحیح، طبیعی و حسابی، عدد گویا نیز هستند.

نماد ریاضی اعداد گویا

مجموعه اعداد گویا معمولاً با حرف Q نمایش داده می‌شوند که به انتخابِ جوزپه پئانو از ابتدای کلمهٔ ایتالیاییِ quoziente، به‌معنای خارج‌قسمت، اخذ شده‌است

تعریف

به‌طور کلی می‌توان مجموعه اعداد گویا را بدین صورت تعریف کرد: اگر ما یک عدد طبیعی داشته باشیم و آن را (مثلا x ) بر دیگری (مثلا y ) تقسیم کنیم؛ به طوری که (یا به شرطی که) هم x (صورت) و هم y (مخرج) عضو مجموعه اعداد صحیح ( Z ) باشند؛ و y (مخرج) برابر با صفر نباشد؛ آنگاه نسبت x به y (کسر مورد نظر) عددی گویا خواهد بود.

[4]  این مجموعه[مجموعه اعداد گویا] خاصیت مهم چگال بودن را دارد. منظور این است که بین هر دو عدد گویای متمایز عدد گویای دیگری در حقیقت بینهایت عدد گویای دیگر - وجود دارد. مثلاً بین ۰ و ۱ اعداد گویای

 1/2 .2/3 .3/4 .4/5 .5/6 .….n/(n+1)

قرار دارند، بین  ۰ و     اعداد گویای

  1/3.2/5.3/7.4/9.5/11….n/(2n+1) 

قرار دارند. (تاریخ ریاضیات، ج ۲، ص ۳۰۳-۳۰۴)

[5] در ریاضیات، یک مجموعه شماراست اگر یا متناهی باشد یا بتوان تناظری یک به یک از آن با مجموعه اعداد طبیعی ایجاد کرد.

معادلاً، یک مجموعه شماراست اگر تابعی یک به یک از آن به اعداد طبیعی وجود داشته باشد؛ یعنی هر عضوی از آن مجموعه باید به عددی طبیعی و اختصاصی مرتبط شود، یا اینکه اعضای آن مجموعه را بتوان یکی یکی شمرد، با اینکه به علت تعداد اعضای نامتناهی، این شمارش هیچگاه نباید پایان یابد.

به بیان حرفه ای تر، با فرض اصل انتخاب شمارا، یک مجموعه شماراست اگر عدد اصلی آن (تعداد اعضای آن مجموعه) نسبت به مجموعه اعداد طبیعی بیشتر نباشد. به مجموعه شمارایی که متناهی نباشد شمارای نامتناهی می‌گویند.

این مفهوم منتسب به جرج کانتور است، کسی که وجود مجموعه های ناشمارا را اثبات کرد، یعنی مجموعه هایی که شمارا نباشند؛ مثلاً مجموعه اعداد حقیقی.

تعریف

مجموعه‌ای را شمارا (قابل شمارش) می‌نامند، که یا متناهی است یا عدد کاردینال آن با کاردینالیتهٔ مجموعهٔ اعداد صحیح و مثبت یکی است. به مجموعه‌ای که شمارش‌پذیر نیست، مجموعهٔ ناشمارا (مجموعهٔ غیرقابل شمارش) گفته می‌شود. به‌هنگامی که یک مجموعهٔ نامتناهی S شمارش‌پذیر است، عدد کاردینال آن با 0 ℵ نشان داده می‌شود.(سایت ویکی پدیا)

در این زمینه همچنین به سایت درآمد به منطق، صفحه مجموعه‌های متناهی، نامتناهی، شمارا، ناشمارا  و مجله رشد ریاضی، مقاله مجموعه‌های متناهی، نامتناهی،  شمارا و ناشمارا مراجعه فرمایید.

[6] در ریاضیات یک تناظر دوسویه (یا تناظر یک به یک) (به انگلیسی: one-to-one correspondence یا bijection) به تابعی میان اعضای دو مجموعه گفته می‌شود به شرط این که هر عضو از هر مجموعه با دقیقاً یک عضو از مجموعه‌ی دیگر جفت شده باشد. در هیچ‌کدام از مجموعه‌ها هیچ عضو بدون جفتی وجود ندارد.

هر تابع دوسویی از مجموعهٔ X به مجموعهٔ Y دارای یک تابع وارون از Y به X است. اگر این دو مجموعه متناهی باشند در این صورت وجود تناظر یک‌به‌یک میان اعضای آن‌ها نشان‌دهندهٔ این است که تعداد اعضای این دو مجموعه برابر است. در مورد مجموعه‌های نامتناهی این تناظرها باعث به وجود آمدن مفهوم اعداد کاردینال شدند که روشی برای بررسی بی‌نهایت‌های متفاوت هستند.

هر تابع دوسویی از یک مجموعه به خود آن مجموعه جایگشت نام دارد.

توابع دوسویی برای بسیاری از مباحث ریاضی ابزاری ضروری هستند. به عنوان مثال: تعاریف یک‌ریختی و همسان‌ریختی.

تعریف

برای این که تابع f از مجموعه X و به مجموعهٔ Y دوسویی باشد باید چهار شرط زیر برقرار باشند:

    هر عضو مجموعهٔ X باید با حداقل یک عضو مجموعهٔ Y جفت‌شده‌باشد،

    هیچ عضو X نباید با بیش از یک عضو Y جفت‌شده‌باشد،

    هر عضو مجموعهٔ Y باید با حداقل یک عضو مجموعهٔ X جفت‌شده‌باشد و

    هیچ عضو Y نباید با بیش از یک عضو X جفت‌شده‌باشد.

شرط‌های یک و دو تضمین می‌کنند که f تابعی با دامنه‌ی X است. شرط‌های یک و دو گاهی به صورت یک شرط هم نوشته می‌شوند: باید هر عضو مجموعهٔ X دقیقاً با یک عضو از مجموعهٔ Y جفت شود. توابعی که شرط سوم را دارا هستند توابع پوشا نام دارند. شرط چهارم هم تعریف توابع یک‌به‌یک است. با توجه به این عبارت می‌توان نتیجه گرفت که یک تابع دوسویی است اگر و فقط اگر هم یک‌به‌یک باشد هم پوشا.

مثال

معلم در کلاس به دانش‌آموزان می‌گوید روی صندلی‌ها بنشینند و مشاهده می‌کند همه دانش‌آموزان نشسته‌اند و تمام صندلی‌ها پر هستند و نتیجه می‌گیرد تعداد دانش‌آموزان و صندلی‌ها برابر است. با بررسی ۴ شرط تعریف می‌توان نتیجه گرفت که با جفت کردن هر دانش‌آموز با صندلیش می‌توان تناظر یک‌به‌یک میان دانش‌آموزان و صندلی‌ها ایجاد کرد:

    تمام دانش‌آموزان نشسته‌اند (هیچ‌کدام سرپا نیست)،

    هیچ دانش‌آموزی روی بیش از یک صندلی ننشسته است.

    تمام صندلی‌ها پر هستند و

    روی هیچ صندلی بیش از یک نفر ننشسته است.

پس میان دانش‌آموزان وصندلی‌ها تناظر یک‌به‌یک برقرار است و در نتیجه تعداد دانش‌آموزان و صندلی‌ها برابر است.

مثال دیگر بازیکنان فوتبال (یا هر ورزش دیگر) و جایگاه آن‌ها در زمین بازی است. اگر ۱۱ بازیکن و ۱۱ جایگاه در ترکیب تیم در نظر بگیریم با جفت کردن هر بازیکن با جایگاهش تناظر به دست می‌آید. چون ۴ شرط فوق برآورده می‌شوند.(سایت ویکی پدیا)

تناظر یک‌به‌یک: اگر A و B دو مجموعه باشند و به ازای هر عضو از A یک عضو از B و به ازای هر عضو از B یک عضو از A وجود داشته باشد، می‌گوییم A و B تناظر یک‌به‌یک دارند و می‌نویسیم: A≈B.

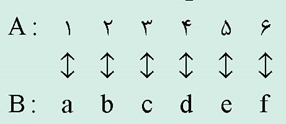
برای مثال، اگر فرض کنیم: A = {۱,۲,۳,۴,۵,۶} و B = {a,b,c,d,f} ، در این صورت واضح است که: A=B. این تناظر یک‌به‌یک را به شکل زیر ملاحظه می‌کنید:

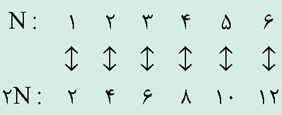
همان‌طور که در تعریف دقت کردید، مفهوم تناظر یک‌به‌یک بین دو مجموعه A و B هیچ محدودیتی برای نامتناهی بودن این دو مجموعه ایجاد نمی‌کند و اگر این مفهوم را به دقت به‌کار ببریم، به سادگی و به‌صورت زیر می‌توان نشان داد که مجموعه عددهای طبیعی و مجموعه عددهای طبیعی زوج تناظر یک‌به‌یک دارند؛ یعنی: N≈۲N

(مجله رشد ریاضی، مقاله مجموعه‌های متناهی، نامتناهی،  شمارا و ناشمارا)

[7] تعداد عنصرهای دو مجموعه متناهی X و Y  برابر است اگر و تنها اگر یک تناظر یک به یک f: X   Y  بین X  و Y  وجود داشته باشد. هرچند که عبارت تساوی تعداد عنصرها را برای حالتی که مجموعه‌های  X  و Y  نامتناهی هستند به کار نمی بریم، به نظر می‌رسد طبیعی باشد فکر کنیم دو مجموعه نامتناهی که در تناظر یک به یک هستند، دارای یک اندازه هستند. ما این ادراک را به‌صورت زیر بیان می‌کنیم:

دو مجموعه X  و Y را همتوان می‌گویند و نماد X    Y    را برای آن به کار می‌برند، هرگاه بین X  و Y  یک تناظر یک به یک f: X   Y  وجود داشته باشد. (نظریّه مجموعه‌ها و کاربردهای آن، ص ۱۲۲)

[8] اعداد ترامتناهی اعدادی نامتناهی‌اند، بدین معنا که آن‌ها بزرگتر از تمام اعداد متناهی‌اند و لزوماً نامتناهی مطلق نیستند. عبارت ترامتناهی (transfinite) توسط جورج کانتور ابداع شد. او می‌خواست که با این کلمه اشاره‌ای ضمنی به کلمهٔ بی‌نهایت کرده باشد، تا بدین شکل بر متناهی نبودنشان اشاره کرده باشد. با این حال برخی از نویسندگان معاصر نسبت به این کلمه مردد هستند؛ اکنون به کار بردن کلمهٔ «بی‌نهایت» برای کاردینال‌ها و اوردینال‌های بی‌نهایت پذیرفته شده‌است. با این حال کلمهٔ ترامتناهی نیز هنوز به کار برده می‌شود.(سایت ویکی پدیا)

[9] سؤال یکی از دوستان حاضر در جلسه درس

[10] در این زمینه به مقاله گردآوری «کاربرد مفاهیم ریاضی در تبیین مفاهیم الهیاتی(۱): عدد پی»  و صفحه عدد پی در سایت فدکیه مراجعه فرمایید.

[11]جلسه یازدهم فقه هوش مصنوعی

[12] در کتاب تاریخ ریاضیات در مورد اعداد ترانسفینی این‌چنین می‌خوانیم:

نظريه ریاضی جدید مجموعه ها یکی از مهمترین ابداعات ذهن بشری است. به دلیل قاطعیت نا معمول برخی از ایده هایی که در آن یافت میشود و به دلیل برخی روشهای ممتاز اثبات ناشی از آن نظریه مجموعه ها جذابیت وصف ناپذیری یافته است ولی بالاتر از همه این نظریه اهمیت بسیار زیادی تقریباً در تمام ریاضیات دارد. این نظریه درغنا، وضوح، توسیع و تعميم بسیاری از زمینه های ریاضیات بی اندازه مؤثر بوده است و نقش آن در مطالعه مبانی ریاضیات کاملا اساسی است. نظریه مجموعه ها همچنین حلقه های ارتباط بین ریاضیات از يك سو و فلسفه و منطق از سوی دیگر را تشکیل می دهد. دو مجموعه را هم ارز گویند اگر و فقط اگر بتوان آنها را در تناظر يك به يك قرار داد.

وقتی دو مجموعه هم ارز باشند می گویند دارای یک عدد اصلی هستند. اعداد اصلی مجموعه های متناهی را میتوان با اعداد طبیعی مشخص کرد. اعداد اصلی مجموعه های نامتناهی به اعداد ترانسفینی معروف اند و نظریه این اعداد اولین بار توسط گئورگ کانتور در يك سرى مقاله قابل توجه که از سال ۱۸۷۴ آغاز شد بسط یافت. اغلب این مقالات در مجله های آلمانی ماتماتیشه آنالن و مجله ریاضیات به چاپ رسیدند. قبل از مطالعه كانتور، رياضيدانان فقط يك بینهایت را پذیرفته بودند که با علامتی شبیه به  نشان داده می شد و این علامت بدون تمایز برای نشان دادن عدد اعضا در مجموعه هایی نظیر مجموعه کلیه اعداد طبیعی ومجموعه كلية اعداد حقیقی به کار گرفته میشد با کار کانتور دیدگاه کاملا جدیدی مطرح گردید و مقیاس و حسابی برای بینهایتها به دست آمد.

 این اصل اساسی که مجموعه های هم ارز عدد اصلی واحدی دارند، در موردی که مجموعه های تحت بررسی مجموعه های نامتناهی باشند وضعیتهای جالب و شگفت آوریپیش می آورد. گالیله پیشتر در نیمه دوم قرن شانزدهم متوجه شده بود که ، به كمك تناظر  n ، مجموعه كليه اعداد صحیح مثبت را میتوان در يك تناظر يك به يك با مجموعه کلیه اعداد صحیح مثبت و زوج قرار داد از اینرو باید به هر یک از این دو مجموعه عدد اصلی واحدی اختصاص داد و ، از این نقطه نظر باید گفت که تعداد اعداد صحیح مثبت برابر تعداد اعداد صحیح مثبت زوج است بی در نگ میتوان مشاهده کرد که اصل موضوع اقلیدسی مبنی بر اینکه کل بزرگتر از جزء است در موقعی که اعداد اصلی مجموعه های نامتناهی مورد بحث اند نمیتواند جایز باشد. در واقع در کیند در حدود  ۱۸۸۸، يك مجموعه نامتناهی را مجموعه ای تعریف کرد که با یک زیر مجموعه حقیقی خودش هم ارز باشد.

ما عدد اصلی مجموعه کلیه اعداد طبیعی را با d  نشان خواهیم داد،( كانتور این عدد اصلی را با حرف عبری الف با اندیس صفر یعنی  نشان داد. پ) و هر مجموعه ای با این عدد اصلی را شمارا خواهیم نامید نتیجه میشود که مجموعه ای مانند که شمار است اگر و فقط اگر اعضای آن را بتوان به صورت دنباله بی پایان (s_₀, s_₁ , s_₂ , …) نوشت. چون به آسانی می توان نشان داد که هر مجموعه نامتناهی زیر مجموعه شما رایی دارد، نتیجه می شود که d «کوچکترین» عدد ترانسفینی است. کانتور در یکی از اولین مقاله های خود درباره نظریه مجموعه ها ، شما را بودن دو مجموعه مهم را که در نگاه اول به زحمت واجد این خاصیت به نظر می رسند، اثبات کرد.

اولین مجموعه ، مجموعه اعداد گویا است. این مجموعه خاصیت مهم چگال بودن را دارد. منظور این است که بین هر دو عدد گویای متمایز عدد گویای دیگری -در حقیقت بینهایت عدد گویای دیگر - وجود دارد.

مثلاً بین ۰ و ۱ اعداد گویای 

 1/2 .2/3 .3/4 .4/5 .5/6 .….n/(n+1)

قرار دارند، بین  ۰ و    ۱  اعداد گویای

 1/3.2/5.3/7.4/9.5/11….n/(2n+1) 

 قرار دارند ….

 به موجب این خاصیت ممکن است این تصور به وجود آید که عدد تر انسفینی مجموعه اعداد گویا بزرگتر ازd است.( عدد اصلی مجموعه ای مانند A را بزرگتر از عدد اصلی مجموعه ای مانند B گویند اگر و فقط اگر B بايك زير مجموعه حقیقی A هم ارز باشد ، ولی A با هیچ زیر مجموعه حقیقی B هم ارز نباشد. پ) کانتور نشان داد که چنین نیست و برعکس،مجموعة اعداد گویا شمار است اثبات آن جالب و به صورت زیر است:

قضیه ۱: مجموعه اعداد گویا شماراست.

…

دومین مجموعه ای که توسط کانتور مطالعه شد ، مجموعه اعدادی است که ظاهراً بسیار وسیعتر از مجموعه اعداد گویاست…

قضیه ٢ مجموعه كليه اعداد جبری شمار است.

با توجه به دو قضیه قبل این امکان باقی میماند که همه مجموعه های نامتناهی شما را هستند. خلاف آن توسط کانتور با برهان اعجاب آوری در قضیه مهم زیر نشان داده شد.

قضية ٣ مجموعه كلیه اعداد حقیقی در بازه 0<x<1ناشماراست.

اثبات به برهان خلف است و روش نامعمولی موسوم به فرایند قطری کردن کانتور را مورد استفاده قرار می دهد. در این صورت فرض میکنیم که مجموعه شمار است. با این فرض میتوان اعداد مجموعه را در دنباله ای مانند  {p₁,p₂,p₃,…} فهرست کرد. هر يك از این اعداد را میتوان به طور منحصر بفردی به صورت يك كسر اعشاری نامختوم نوشت ؛ در این رابطه یادآوری این مطلب مفید است که هر عدد گویا را میتوان به صورت «اعشاری مکرر نوشت؛ مثلا عددی مانند 0.3 را می توان به صورت 0.299999… نوشت. در این صورت میتوانیم دنباله را با آرایه زیر نمایش دهیم:

P₁=0.a₁₁ a₁₂ a₁₃…

P₂=0.a₂₁ a₂₂ a₂₃…

P₃=0.a₃₁ a₃₂ a₃₃…

که در آن a_{i j} به معرف یکی از ارقام ۱۰، ۲، ۳، ۴، ۵ ، ۶، ۷، ۸، ۹ است . حال علیرغم دقتی که در فهرست کردن کلیه اعداد بین ۰ و ۱ به کار رفته است عددی وجود دارد که نمی توانسته در فهرست وارد شود چنین عددی0.b ₁  b ₂  b _3… است که در آن، مثلاً7 = b_k در صورتی که a_kk 7   و  3=b_k اگر a_kk 7    به ازای هر  1,2,…n…= k.

این عدد آشکارا بین ۰ و ۱ قرار دارد و باید با هر يك از اعداد p متفاوت باشد، زیرا با P₁حداقل در رقم اعشاری اول تفاوت دارد، با P₂ حداقل در رقم اعشاری دوم تفاوت دارد، با P₃حداقل در رقم اعشاری سوم تفاوت دارد، و الی آخر. بدین ترتیب فرض آغازین که همه اعداد حقیقی بین ۰ و ۱ را میتوان در دنباله ای فهرست کرد ، قابل قبول نیست، ولذا این مجموعه باید ناشمارا باشد.

كانتور قضیه مهم زیر را از قضایای ۲ و ۳ نتیجه گرفت:

قضيه ۴ اعداد متعالی موجودند.

چون بنا بر قضیه ۳ مجموعه اعداد حقیقی بین ۱و۰ ناشماراست، به آسانی می توان نشان داد که مجموعه اعداد مختلط نیز نا شماراست. اما بنا بر قضیه ۲ مجموعه اعداد جبری شمار است. نتیجه میشود که باید اعداد مختلط که جبری نیستند وجود داشته باشند و قضیه ثابت می شود. برهان فوق برای قضیه ۴ برای همه ریاضیدانان قابل قبول نیست. قابل قبول بودن یا غیر قابل قبول بودن این برهان مربوط به تصور ما از چگونگی وجود ریاضی است و ریاضیدانانی وجود دارند که به زعم آنها وجود ریاضی فقط موقعی ثابت میشود که یکی از چیزهایی که وجودشان مورد بحث است عملا ساخته و نشان داده شود. ولی برهان بالا وجود اعداد متعالی را با ایجاد نمونه مشخصی از چنین اعداد ثابت نمی کند. در ریاضیات برهانهای وجودی از این نوع غیر ساختنی فراوان اند که در آنها وجود، فرضاً تنها با نشان دادن اینکه فرض عدم وجود منجر به تناقض میشود، ثابت میگردد . مثلا بسیاری از براهین قضیه اساسی جبر بر چنین اساسی فرمولبندی شده اند. به دلیل ناخشنودی برخی ریاضیدانان از برهانهای وجودی غیر ساختنی، تلاش زیادی صرف جانشین کردن این برهانها با برهانهایی شده است که عملاً یکی از چیزهای مورد بحث را می دهند.

 اثبات وجود اعداد متعالی و این اثبات که عدد خاصی متعالی است دو مطلب کاملا متفاوت اند. دو می اغلب مسئله بسیار دشواری است. ارمیت در سال ۱۸۷۳، ثابت کرد که عدد e، پایه لگاریتم طبیعی متعالی است. لیندمان ، در سال ۱۸۸۲، برای اولین بار متعالی بودن  را ثابت کرد. متأسفانه برای اثبات این حقایق جالب در این کتاب محذوراتی وجود دارد. دشواری مشخص کردن جبری بودن یا متعالی بودن عدد مفروض خاصی را می توان با این حقیقت روشن کرد که هنوز معلوم نیست که جبری یا متعالی است . دستاورد جدیدی در این زمینه اثبات ماهیت متعالی بودن اعدادی به شکل  است که در آن a عددی جبری جز ۰ و ۱ است و b يك عددنا گویای جبری میباشد این نتیجه که در سال ۱۹۳۴ توسط الکساندر او سیپوویچ گلفوند (متولد۱۹۰۶) به دست آمده و امروزه قضیه گلفوند نامیده می شود حاصل کوشش تقریباً ۳۰ ساله ای برای اثبات متعالی بودن به اصطلاح  عدد هیلبرت ، 2  بوده است.

چون مجموعه همه اعداد حقیقی در بازه 0<x<1 ناشمار است، عدد تر انسفینی این مجموعه بزرگتر از d است. ما آن را با c  نشان میدهیم و آن را عدد اصلی متصله اطلاق می کنیم. عقیده کلی بر این است که c عدد ترانسفینی بعد از d است، یعنی اینکه هیچ مجموعه ای نیست که دارای عدد اصلیی بزرگتر از d و کوچکتر از c باشد. این اعتقاد به فرض متصله موسوم است ولی علی رغم کوششهای شدید هنوز برهانی برای آن پیدا نشده است. نتایج زیادی از این فرض استنتاج شده اند و به حدود سال ۱۹۴۰، منطقی اطریشی کورت گودل (۱۹۰۶) - (۱۹۷۸) به اثبات این نکته موفق شد که فرض متصله با مجموعة اصول موضوعه مشهوری مربوط به نظریه مجموعه ها سازگار است به شرطی که خود این اصول موضوعه سازگار باشند. گودل حدس زد که انکار فرض متصله نیز با اصول موضوعه نظريه مجموعه ها سازگار است. این حدس را در سال ۱۹۶۳ دکتر پل. ج. کوهن از دانشگاه استانفورد ثابت کرد و بدین ترتیب نشان داد که فرض متصله از اصول موضوعه نظريه مجموعه ها مستقل است و بنا بر این قابل استنتاج از این اصول موضوعه نیست. این وضعیت شبیه به وضعیت اصل توازی در هندسه اقلیدسی است.

نشان داده شده است که مجموعه کلیه توابع تك مقداری مانند (x)f₁  که بر بازه0<x<1 تعریف شده اند، دارای عدد اصلی بزرگتر از c هستند ولی اینکه آیا عدد اصلی مزبور عدد بعد از c هست یا نیست معلوم نشده است. نظریه کانتور دنباله نامتناهیی از اعداد ترانسفینی را پیش بینی میکند و براهینی وجود دارند که مقصودشان نشان دادن آن است که تعداد نامحدودی از اعداد اصلی بزرگتر از متصله عملاً موجودند. (تاریخ ریاضیات، ج ۲، ص ۳۰۲-۳۰۷)