١.عدد پی
بی نهایت
ما بینهایتهای بی در و پیکر خیلی داریم. انسان خودش را قانع میکند به بی نهایتِ لا یقفی[1]؛ تمام میشود. اما دو نوع بینهایت درست و حسابی، داریم: بینهایتهای متعیّن افزایشی، بینهایتهای متعیّن کاهشی؛ بی نهایت های بسیار بزرگ ، بی نهایت های بسیار کوچک[2] .
از زمان ارسطو، تمام بی نهایت ها؛چه بی نهایت بزرگ و چه بی نهایت کوچیک را با بی نهایت بالقوه، حلش می کردند. بی نهایت بزرگ را می گفتند: لایقف . بی نهایت کوچک را می گفتند: بالقوه . ما هم با این دوتا خیلی مانوس هستیم چون مبنای کتابهای ما هم معمولا ارسطویی است.
اما از حدود ۲۰۰ سال قبل تا حالا که ریاضیات عالی و آنالیز[3] کاملا پیشرفت کرده و مباحثش امروز برای بشر مثل خورشید شده امروز واضح است که در بی نهایت کوچک، بی نهایتِ بالفعلِ نفس الامری است.می توانم بگویم بینهایتِ مجسّم. بینهایتِ در مشت. میگوید بیا، بینهایتِ بالفعل را در مشتت میگذارم، جلوی چشمت میآورم، بالاتر از این میخواهی؟
تحلیل اجزاء دایره
آن وقت این هم انواعی دارد. یک مثال روشنش، عدد پی( )[4] است. عدد پی، عددی هندسی است، یعنی شما اوّل سروکارتان با دایره میشود. دایره چیست؟ یک خطِّ بستهی منحنی. خط برای کجاست؟ برای هندسه است. کمّ متصل قارّ. بعد میگویید دایره یک مرکز دارد. مرکز، نقطه است. نقطه، عنصر هندسی است. قطر چیست؟ خط مستقیمی که از مرکز رد میشود و دایره را دو قسمتش میکند. این خطّ مستقیم، طول است؛ کم متصل قارّ است.
عدد پی:نسبت محیط دایره به قطر
میخواهیم ببینیم نسبت محیط دایره به قطر چقدر است؟ یعنی اگر محیط را باز کنیم، از گِردی در بیاوریم و یک خطِّ مستقیمش بکنیم، چند تا قطر بگذاریم سر میرسد؟ می گوییم سه تا قطر را که روی محیط بغلطانید دایره، می گردد، دفعه بعدش دیگر نه؛ کمی از آن فقط میماند. این را میگوییم نسبت محیط به قطر، یعنی محیط، چند برابر قطر است؛ نسبت یعنی صورت، تقسیم بر مخرج. یعنی محیطِ گردِ دایره، تقسیم بر قطر، می شود عدد پی.فعلاً می گوییم ۳.۱۴.
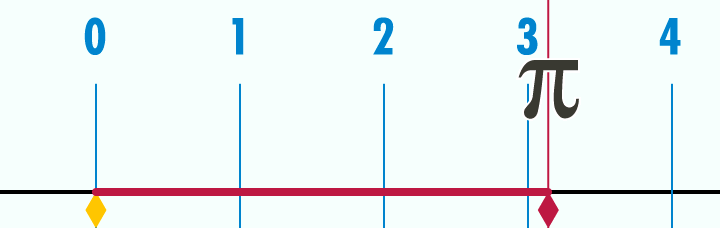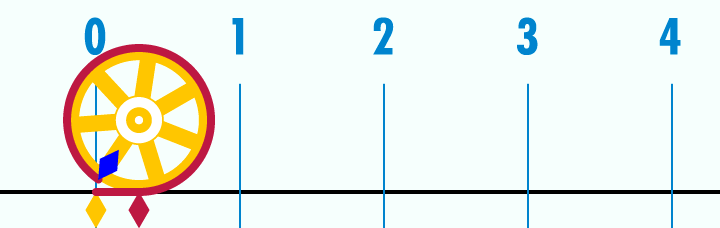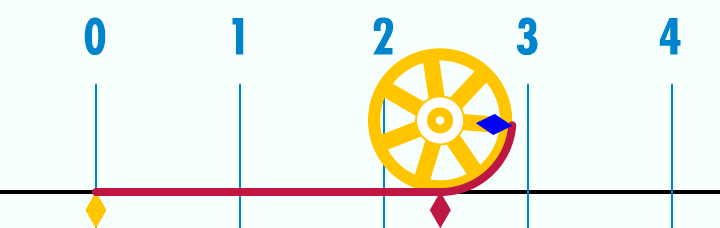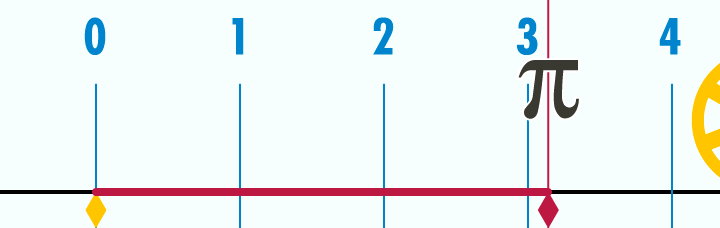
هر دایره دلخواه –که دایره هندسی باشد- را روی هر محوری رسم کنید، به محض اینکه روی محور اعداد، این دایره را باز کنید، اگر قطر این دایره،١ باشد(«یکِ» رویِ محور) یک سر محیط دایره را روی عدد صفر میگذارید، آن سرِ محیط میشود عدد پی[5]. یک نقطهی معیّن روی محور؛سه و چهارده صدم و ...بروید تا بینهایت. نقطهاش روی محور معلوم است.[6]
عدد پی، عددی است که روی نقطه معیّنی روی محور است، اما شما نمیتوانید نشانش بدهید. چه کار میکنید؟ از پس و پیش، به آن نزدیک میشوید. یعنی از ۳.۱۴ که مثلاً با ۹۶ ضلعی ارشمیدس بوده[7]، از نقطه ۳.۱۴ شروع میکنید، بعد از ۳.۱۴ روی محور، ۳.۱۵ است. میگویید نقطه پی که محیط دایره است، بین ۳.۱۴ و ۳.۱۵ هست. نه بیرون از ۳.۱۵ است، نه عقبتر از ۳.۱۴ است؛ بین این دو تاست. از طرفین(۳.۱۵ و ۳.۱۴ )به آن نزدیکتر میشوید وتا بینهایت میروید. حدّش[8] هست. به تعبیر مسامحی میگوییم در بینهایت به پی میل میکند.
امروز دیگر اینها از واضحات است، یعنی اهل خبره دو نفرشان هم در این اختلاف ندارند، امروز برای بشر، این که عدد پی عددی است گنگ[9]، متعالی[10]و رسمناپذیر[11]، مبرهن شده است[12].
خوب دقت کنید.الآن عددهای بعد ۱۴ صدُم را؛ممیّزهای بعد ممیّز را، تا چندین تریلیون حساب کردند[13]. خلاصه آخرین عددی که فعلاً بشر میداند، میدانیم یک عددی معیّن بعدش هست؛ ما نمیدانیم، ولی معیّن است. ما باید برویم کشفش کنیم؛ نه فرضش کنیم؛ نه خلقش کنیم .نکته اصلی این است، این نقاطی که شما بعد از ممیّز میگذارید، نقطهای معیّن روی محور است؛ نقطهی نامعین نیست. یعنی ۳.۱۴ که معین است، عدد بعدی ممیز که ۳.۱۴۱، روی محور معلوم است، ولو نزدیکتر به پی شده ولی خود پی نیست. عدد بعدی هم همینطور، تا بینهایت میروید ولی به سر دایره نمیرسید، چون عدد گنگ است. ولی نقاطی که طی میکنید تا به آن نزدیک بشوید نقاط متعین است.
بی نهایت؛قابل ارائه به بچه دبستانی
این است که میگویم زمینهاش فراهم است که برای بشر نشان بدهیم. الآن شما یک دایره را باز کردید، کف دست بچه میگذارید. میگویید این سر «پی» که معلوم است، صفر هم معلوم است. وقتی میخواهی حساب کنی بروی برسی به سر دایره که پی است، در رسیدن به نقطهی پی، بینهایت نقطهی متعیّن است که هر چه حساب پی را جلوتر ببرید کشفش میکنید.دو طرف، بینهایت. یعنی از دو طرف دارید به آن نقطه پی نزدیک میشوید تا بینهایت هم در بینهایت نزدیک میشوید، نقاطش هم متعین است، شما کشفش میکنید؛ ولی در عین حال هیچکدام از آنها «پی» نیست!این،یک مثالِ هندسیِ ساده است، هر بچهای هم در دبستان خوانده است. میخواهیم چیزهایی را که همه بلد هستند فقط به او نشان بدهیم.
الان این مثال،مثل سنگ خاراست، فقط باید کار بشود و این مثالها باز بشود،تصویری توضیح داده بشود، که همه بفهمند. وقتی اذهان مطلب را گرفتند، همینطور دست به دست میشود؛ به سرعت پخش میشود.
[1] تناهى به دو معناست: يكى تناهى عددى، و ديگر تناهى لا يقفى. نامتناهى عددى آن است كه شىء بالفعل موجود و نامتناهى باشد، مثلا خط و سطح و جسم بالفعل موجود باشد و نهايت نداشته باشد. و نامتناهى لا يقفى آن است كه بالفعل موجود نباشد، بلكه به هر مرتبه كه رسد باز در آن چيزى بتوان فرض نمود.چنانچه حكما گويند كه جسم قابل قسمت است الى غير النهاية، كه هر اندازه جسم را تقسيم كنيم باز هم قابل قسمت است و به انتهاء نمىرسد. و اينكه حكما گويند نامتناهى وجود ندارد مقصود نامتناهى عددى است، ولى نامتناهى لايقفى جائز و واقع است، مثل اينكه جسم به نامتناهى تقسيم مىشود و اين قسمتها به جايى نمىرسند كه ديگر تقسيم نشوند. حكماى قديم يونان مىگفتند ابعاد نامتناهى است.(مجموعه رسائل عرفانی و فلسفی،ص ٢۶٩)
[2] بینهایت کوچکها، کمیتهایی هستند که بیش از هر عدد حقیقی استانداردی به صفر نزدیک اند ولی صفر نیستند. این اعداد در مجموعهٔ اعداد حقیقی معمول وجود ندارند ولی در سیستمهای عدد دیگر مثل اعداد سورئال و اعداد ابرحقیقی وجود دارد.(سایت ویکی پدیا)
[3] آنالیز، آنالس به انگلیسی: (Analysis)، واکافت، واکاوی یا تجزیه و تحلیل شکستن یک مجموعه به بخشهای کوچک برای فهم بهتر آن است. به عبارت دیگر، آنالیز، تجزیه و تحلیل دادهها برای گرفتن نتیجهٔ پیچیدهتر نیز میتواند باشد.
در دانش شیمی، آنالیز به تجزیه نمونه و بررسی آن اطلاق میشود که در شاخه شیمی تجزیه دنبال میگردد. در دانش ریاضیات و آمار، آنالیز به بررسی احتمالات و ریزحالتها میپردازد. (سایت ویکی پدیا)
[4] عدد پی (π) (به انگلیسی: Pi) از عددهای ثابت ریاضی و تقریباً برابر با ۳٫۱۴ است. این عدد را با علامت π نشان میدهند. عدد پی عددی حقیقی و گُنگ است که نسبت محیط دایره به قطر آن را در هندسهٔ اقلیدسی مشخص میکند و کاربردهای فراوانی در ریاضیات، فیزیک و مهندسی دارد. عدد پی همچنین به ثابت ارشمیدس نیز معروف است .پی،حرف اول کلمهٔ یونانی «پریمتروس» (به معنی محیط) است.(همان)
[6] https://upload.wikimedia.org/wikipedia/commons/2/2a/Pi-unrolled-720.gif
[7] ارشمیدس محیط دایره را نمیدانست؛ اما ناامید نشد و از آنچه میدانست یعنی محیط یک مربع آغاز کرد. البته او در واقع با یک ششضلعی محاسبه خود را آغاز کرد؛ اما از آنجا که ترسیم و کار کردن با مربع آسانتر است، ما از مربع استفاده میکنیم.
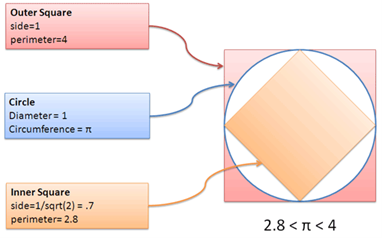
ما محیط یک دایره را نمیدانیم؛ اما میتوانیم آن را بین دو مربع[محیطی و محاطی] رسم کنیم:
دقت کنید که این وضعیت شبیه مسیر مسابقهای با یالهای داخلی و خارجی است. محیط دایره هر چه که باشد بین محیط دو مربع قرار دارد، یعنی بیشتر از محیط مربع داخلی و کمتر از محیط مربع بیرونی است.محیط مربعها را میتوانیم به سادگی محاسبه کنیم:ما نمیدانیم که پی چقدر است؛ اما میدانیم که عددی بین 2.8 و 4 است. اگر تصور کنیم دقیقاً نیمه این دو کرانه باشد، پس باید در حدود 3.4 باشد.
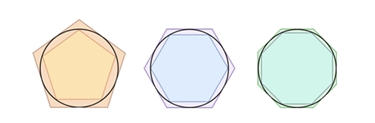
مربعها گوشهدار هستند. آنها را نمیتوان چندان شبیه دایره دانست و این اختلاف موجب محاسبات نادرست و با اشتباه زیاد میشود؛ اما با افزایش اضلاع، برای مثال با استفاده از هشتضلعی میتوانیم حدس بهتری از عدد پی داشته باشیم.
چنان که میبینید با افزایش تعداد اضلاع، به شکل یک دایره نزدیکتر میشویم. متأسفانه اعداد اعشاری در سال 250 قبل از میلاد هنوز اختراع نشده بودند، چه برسد به نرمافزارهای صفحه گسترده. بنابراین ارشمیدس مجبور بود که این فرمولها را به کمک کسرها حل کند. او کار خود را با ششضلعی آغاز کرد و با ١٢، 24، 48 و 96 ضلع ادامه داد. تخمین نهایی وی از عدد پی با استفاده از شکلی با 96 ضلع به صورت زیر بود:
نقطه میانی این بازه برابر با 3.14185 است که تقریباً 99.9% دقیق است!(سایت فرادرس،مقاله عدد پی چگونه کشف شد؟)
[8] حد (به انگلیسی:( Limit): وقتی که مقادیر متوالی به یک متغیر نسبت داده میشود، و آن متغیر بینهایت به عدد ثابتی نزدیک شود، به طوری که اختلاف آنها از مقدار ثابت به هر اندازه کوچک قابل انتخاب باشد، این مقدار ثابت را حد همه مقادیر متغیر میگویند.(سایت ویکی پدیا)
[9] عدد غیر نسبی، گُنگ یا اصم به انگلیسی:( Irrational number) در دستگاه اعداد بهصورت عددی حقیقی تعریف میشود که عدد نسبی (عدد گویا(نباشد، یعنی نتوان آن را به صورت کسری نوشت که صورت و مخرجش عدد صحیح باشند.(همان)
[10] اعداد گنگ دو نوع دارند: اعداد جبری (algebraic numbers) و اعداد متعالی (transcendental numbers)
هر عدد جبری به عنوان راه حل حداقل یک معادله چند جمله ای، نشان داده می شود. برای مثال، فرض کنید معادله زیر را دارید:
شما می توانید این معادله را به شکل زیر حل کنید:
بنابراین 2√ یک عدد جبری می باشد که مقدار تقریبی آن برابر با ...1.4142135623 است.
یک عدد متعالی (transcendental number)، در مقایسه با یک عدد جبری، هرگز راه حل یک معادله چند جمله ای نمی باشد(سایت خوشآموز،مقاله ده مجموعه مهم اعداد که باید بشناسید)
[11] عدد a را «رسم پذیر» گوییم اگر بتوان تنها با استفاده از خط کش و پرگار پاره خطی به طول a رسم کرد. و البته فرض ما بر این است که یک واحد طول داده شده باشد.از این به بعد هر جا کلمه رسم پذیری آمد منظور همان، رسم پذیری به وسیله خط کش و پرگار است.رسم پذیری بعضی عددها بسیار واضح است. مثلا ۱ و ۲ و ... اما بعضی دیگر احتیاج به بررسی دارند مثل 2√ . آیا این عدد رسم پذیر است؟
از دوران دبیرستان به یاد داریم که : از هر نقطه خارج یک خط مفروض می توان خطی عمود بر آن رسم کرد.اگر محل تلاقی این دو خط را مبدأ،در نظر بگیریم به این محور، محور رسم پذیر می گوییم.
در این محور:
۱(a,0)يا(0,a) را رسم پذیر گوییم اگر a رسم پذیر باشد.
۲) (a,b) را رسم پذیر گوییم اگر a و b رسم پذیر باشند.
هر شکلی را که روی این محور بتوان رسم کرد، اعم از پاره خط، دایره و... یک شکل رسم پذیر گوییم. حال می توانیم به راحتی بگوییم که 2√رسم پذیر است. چون اگر(۰.۱)و (۰و۱) را روی محور به هم وصل کنیم بنابر قضیه فیثاغورث پاره خطی به طول 2√داریم. حال سوالی که مطرح می شود این است که آیا همه اعداد رسم پذیرند؟ و اگر نه چه عددهایی رسم پذیرند و کدام ها رسم پذیر نیستند. همه عددها رسم پذیر نیستند و تعیین رسم پذیری آنها به کارهای تخصصی می انجامد.(دانشنامه رشد،رسم پذیر بودن یک عدد)
[12] در سال ۱۷۶۱ لامبرت ریاضیدان سوئیسی ثابت کرد که عدد پی گنگ است و نمیتوان آن را به صورت نسبت دو عدد صحیح نوشت. همچنین در سال ۱۸۸۲ فردیناند فون لیندمان ثابت کرد که عدد پی یک عدد جبری نیست و نمیتواند ریشه یک معادله جبری باشد که ضرایب آن گویا هستند (همانند عدد (e) )کشف گنگ بودن عدد پی، به سالها تلاش ریاضیدانان برای تربیع دایره پایان داد.(سایت ویکی پدیا)
[13] باوجود آنکه همه ریاضیدانان میدانند که عدد پی گنگ میباشد و هرگز نمیتوان آن را بهطور دقیق محاسبه کرد اما ارائه فرمولها و مدلهای محاسبه عدد پی هموار برای آنها از جذابیت زیادی برخوردار بودهاست. بسیاری از آنها تمام عمر خود را صرف محاسبه ارقام این عدد زیبا نمودند اما آنها هرگز نتوانستند تا قبل از ساخت کامپیوتر این عدد را بیش از ۱۰۰۰ رقم اعشار محاسبه نمایند. امروزه مقدار عدد پی با استفاده از پیشرفتهترین رایانهها تا میلیونها رقم محاسبه شدهاست؛ و تعداد این ارقام هنوز در حال افزایش است. اولین محاسبه کامپیوتری در سال ۱۹۴۹ انجام گرفت و این عدد را تا ۲۰۰۰ رقم محاسبه نمود و در اواخر سال ۱۹۹۹ یکی از سوپر کامپیوترهای دانشگاه توکیو این عدد را تا ۲۰۶٬۱۵۸٬۴۳۰٬۰۰۰ رقم اعشار محاسبه نمود. (همان) آخرین رقم اعشار محاسبه شده، به عدد ۳۱ تریلیون رسیده است.

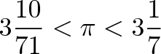
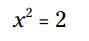
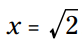
بدون نظر