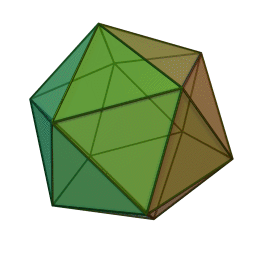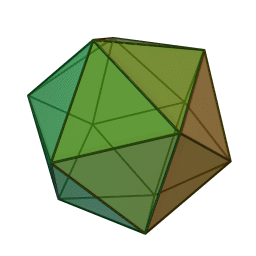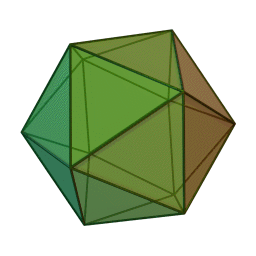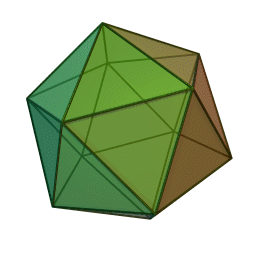
٢.اجسام پنج گانه افلاطونی

یکی دیگر که اشاره می‌کنم برای آنهایی که همت کاری دارند برای بعدها، مسئله­ی اجسام پنج گانه­یِ لایزید و لا ینقص افلاطونی[1] است. چون در هندسه مجسم[2]، اجسامی که می‌تواند از منتظمات تشکیل بشود بیشتر از ۵ تا ممکن نیست: ۴ وجهی، ۶ وجهی، ۸ وجهی، ۱۲ وجهی و ۲۰ وجهی.  شما  می‌توانید بی‌نهایت  شکل منتظم درست کنید. کثیر الاضلاع منتظم[3]. امّا در اجسام، فقط ۵ تا. البته اشکال ارشمیدسی هست، مجسّمات ارشمیدسی[4]. ارشمیدس از منتظم‌های غیرِ هم نوع، این اجسام را درست کرده است .این مطلبی است که فقط اشاره می‌کنم و رد می‌شوم، شما بعداً خواستید روی آن تأمل کنید، ببینید روی مجسّمات افلاطونی، ارشمیدسی، امثال اینها می‌شود مثال‌هایی پیدا کرد برای نشان دادن مثال منفصل یا نه؟ فعلاً با تحلیلی که عرض کردم نمی‌شود؛ چون خود همین اجسام افلاطونی هم پشتوانه‌اش معانی است که عقل درک می‌کند. خود آنها را ما فعلاً چیزی نداریم نشان بدهیم به عنوان مثال منفصل، ان‌شاءالله بیشتر از این، روی این ها کار بشود.

[1] در هندسه فضایی، چندوجهی‌های منتظمِ محدب به جسم افلاطونی موسومند. می‌توان نشان داد که در فضای سه‌بعدی تنها پنج جسم افلاطونی هست، که عبارتند از:

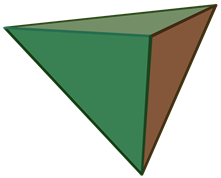
چهاروجهی منتظم، متشکل از چهار مثلث متساوی‌الاضلاع،

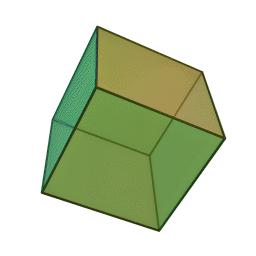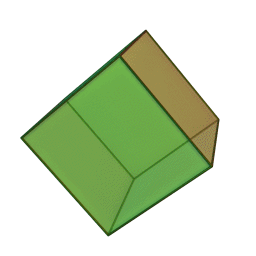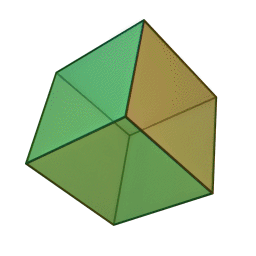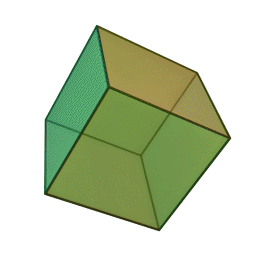
شش‌وجهی منتظم (مکعب)، متشکل از شش مربع،

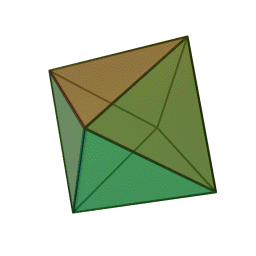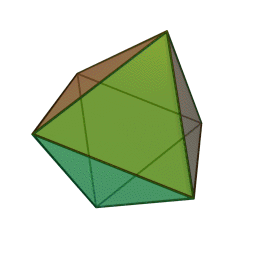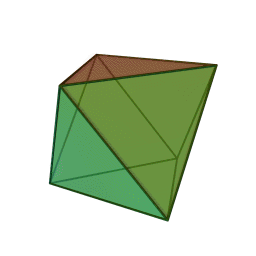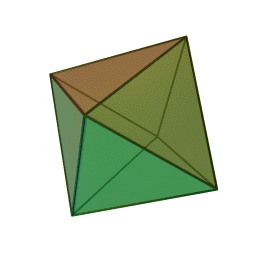
هشت‌وجهی منتظم، متشکل از هشت مثلث متساوی‌الاضلاع،

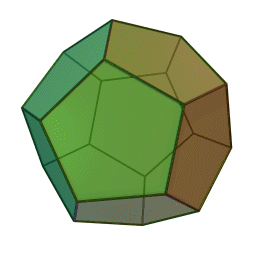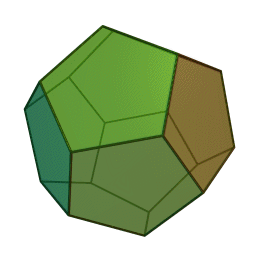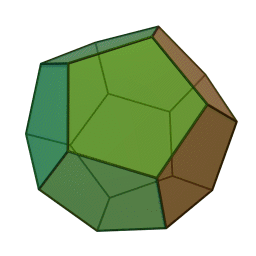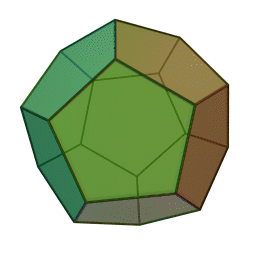
دوازده‌وجهی منتظم، متشکل از دوازده پنج‌ضلعی منتظم،

بیست‌وجهی منتظم، متشکل از بیست مثلث متساوی‌الاضلاع.

وجه‌های هر کدام از این چندوجهی‌ها چندضلعی‌هایی منتظم و هم‌نهشتند و تعداد یکسانی از وجه‌ها در هر رأس آنان به یکدیگر می‌رسند. شش‌وجهی منتظم (مکعب) با هشت‌وجهی منتظم، دوازده‌وجهی منتظم با بیست‌وجهی منتظم، و چهاروجهی منتظم با خودش مزدوجند؛ یعنی با وصل کردن نقطهٔ وسط وجه‌های یکی می‌توان دیگری را ساخت. همچنین در ساخت دوازده‌وجهی منتظم و بیست‌وجهی منتظم نسبت طلایی پدید می‌آید. نخستین مطالعهٔ نظام‌مند دربارهٔ اجسام افلاطونی را فیثاغوری‌های یونان باستان انجام دادندایشان بر این باور بودند که پنج جسم افلاطونی متناظر با ساختار عناصر چهارگانهٔ سازنده جهان هستند، یعنی چهاروجهی منتظم با نوک‌های تیز متناظر آتش، مکعبِ استوار متناظر خاک، و دو چندوجهی منتظم ساخته‌شده از مثلث دیگر (هشت‌وجهی منتظم و بیست‌وجهی منتظم) متناظر هوا و آب هستند. به باور ایشان دوازده‌وجهی منتظم نیز به شکلی مرموز نمایانگر کل هستی و ۱۲ صورت فلکی‌اش بود. خود فیثاغورث (حدود ۵۸۰ تا ۵۰۰ پ.م.) احتمالاً چهاروجهی منتظم، مکعب، و دوازده‌وجهی منتظم را می‌شناخت. او ۲۰ سال را در مصر گذرانده بود و احتمالاً این اطلاعات را آنجا آموخته بود .

تحلیل ویژگی‌های اجسام افلاطونی و اثبات اینکه تنها پنج جسم افلاطونی وجود دارد نقطهٔ اوج کتاب پایانی اصول اقلیدس (حدود ۳۰۰ پ.م.) است. به نوشتهٔ اقلیدس، اولین کسی که هشت‌وجهی و بیست‌وجهی منتظم را شرح داد تئائتتوس ریاضی‌دان آتنی و دوست افلاطون (حدود ۴۱۷–۳۶۹ پ.م.) بود از آنجا که افلاطون (۴۲۸/۴۲۷–۳۴۸/۳۴۷ پ.م.) نظریات فیثاغوری‌ها را در «داستان آفرینش» در دیالوگ تیمائوس تکرار کرده است، نام «جسم افلاطونی» به چندوجهی‌های منتظم اطلاق گردید(همان)

[2] هندسهٔ فضایی (Solid geometry) به هندسهٔ اقلیدسی در فضای سه‌بعدی اطلاق می‌شود. فضایی که در آن جدا از طول و عرض، ارتفاع نیز وجود دارد. هندسهٔ فضایی تا حدود زیادی نیاز به تصورات بالا دارد. کل جهان اطراف ما به صورت سه بعدی و فضایی است. هر حجمی را که می شناسید باید ویژگیهایش در مبحث هندسهٔ فضایی محاسبه شود. اشکالی چون کره، مخروط، و استوانه از این دسته هستند.(همان)

[3] در هندسه اقلیدسی، یک چندضلعی منتظم، چندضلعی است که همه زوایا و اضلاع آن هم‌اندازه‌اند.(همان)

[4] در هندسه، جسم ارشمیدسی )انگلیسی:( Archimedean solid‎جسمی است که همه وجوه آن چندضلعی‌های منتظم اند هرچند همگی لزوماً از یک نوع نیستند و همه زوایای چندوجهی آن باهم برابرند. تعداد این جسم‌ها ۱۳ تاست. این اجسام به نام ارشمیدس، که همهٔ آنها را تعریف کرد نامگذاری شده‌اند. (همان)