٣.نقطه طلایی
هر خطی شما در نظر بگیرید، به هر اندازهای به هر شکلی، یک نقطه طلایی[1] دارد؛ ما باشیم یا نباشیم؛ بلا استثناء. این هم یکی از ثابتهای زیبای هندسی است[2]. اقلیدس، از ۱۰۰۰ سال پیشتر ثابت کرده است[3]. الآن هم بشر خیلی کارها روی این انجام میدهند[4]. ما اگر قوس بزنیم و رسم کنیم کشفش میکنیم[5].
یک نقطهی ثابت است. به محض اینکه مقدارش را عوض کنیم ،جایش عوض میشود. خط ده سانتی، یک نقطهی طلایی دارد مختصّ خودش.آن را ۹ سانت و نیم بکنید ، نقطه طلاییاش عوض میشود. و برایش هم ثابت است. دائماً نقطهی طلایی، خط را به دو بخش تقسیم میکند، بخش بزرگ و کوچک. قسمت اکبر، قسمت اصغر. در حساب هم اگر بیایید می گویند نسبت طلایی.[6]
وجه طلایی بودن نقطهی طلایی
طلایی بودن این نقطه برای این است که مربّعِ بخش بزرگتر، مساحتش مساوی است با مستطیلی که کلّ این خط در آن قسمت کوچکتر تشکیل می دهد. یعنی مستطیل درست کنید، طولش کلّ خط است، عرضش آن قسمت کوچکتر است. مربّعِ بخشِ بزرگتر، مساوی است با مستطیلی که طولش کلِّ خط است؛ عرضش آن قسمت کوچکتر است. این نقطه دارد خط ما را تقسیم میکند. قسمت کوچکتر میشود عرض مستطیلی که طولش کلِّ خط است. قسمت بزرگتر، یک مربع؛ خودش ضرب در خودش. این نقطه را میگویند نقطه طلایی.
انواع ابهام
ابهام دو نوع داریم: یکی ابهام واقعی در متن آن شیء منفصل، یکی ابهام به معنای غضّ نظر ذهن متّصل.وقتی شما میگویید نسبت محیط دایره به قطر، این محیط طول دارد یا ندارد؟ میگویید دارد. چقدر است؟ میگویید مبهم است. مبهم است یعنی ما غضّ نظر میکنیم؟ یا نه واقعاً این طولی که نسبتش را با قطر میسنجیم مبهم است؟
اگر بگوییم که یک عالم مثال منفصلی داریم که از حیث تجرد ، تضاد در آن مانعی ندارد. یعنی میتواند در عین حالی که درجهای از تشکّل و آثار ماده را دارد، درجهای از مضیقههای عالم ناسوتی را نداشته باشد. بُعد داشته باشد؛ اما بُعد نامعین-مجرّد چه طور است؟ یک سعهای دارد از حیث بُعد- در این صورت میگوییم یک موجود منفصلی داریم مثالی، بُعد دارد، اما بُعدی که از یک درجهای از تجرد برخوردار است که محتاج به تشخص بُعد نیست. اگر این را بپذیریم. اما ما فعلاً نیازی نداریم.
ما معانی داریم که آن معانی پشتوانه این اشکال و این چیزهای هندسی است.، بنابراین وقتی میگوییم دایرهای که کذاست، این را دارد با یک قضیه شرطیه درستش میکند؛ معانی را میریزد در یک قضیه شرطیه، آن را بیان میکند. میگوید معنای محیط طول ندارد، معنای طول هم طول ندارد. اما عقل این معنا را که یک معنای عقلانی است، به صورت قضیه شرطیه در ظرف وجود، میگوید که اگر این معنای طول که خودش طول ندارد در ظرف وجود بیاید؛ در ظرفِ قوهی خیال بیاید، آن وقت طول دارد. در این قضیه شرطیه، ما نیازی به طول نداریم. چرا؟ چون قضیه شرطیه این است که اگر طول محیط در ظرف وجود بیاید، نسبتی دارد با طولِ قطر.پس ما به یک موجود منفصل مثالی در این تحلیل نیاز نداریم؛ بلکه به یک معقول منفصل، نیاز داریم. معقولِ منفصلِ ما این است که همهی این معانی با این قضیهی شرطیه (که اگر در ظرف تجرد برزخی مثالی موجود شود، یا اگر در ظرف وجود فیزیکی موجود شود) آنجا که موجود شد مقدار خاصّ خودش را دارد. در اینجا مقدارِ مبهم معنا ندارد. ولی مبهم در قضیه یعنی چه؟ یعنی غضّ نظر. قابل انطباق است بر همه افراد خیالیه یا خارجیه.
[1] بر اساس تناسبات طلایی،یک پاره خط را می توان طوری به دو قسمت تقسیم کرد که نسبت قسمت کوچک تر به قست برزگ تر مساوی با نسبت قسمت بزرگ تر با کل پاره خط باشد.این نوع تقسیم از نظر بصری و همین طور از نظر منطقی،نسبت های زیبایی را میان اجزا با یکدیگر و با کل پدید می آورد که هم در معماری و هم در هنرهای بصری از آن استفاده بسیار شده است.(مبانی هنرهای تجسمی،ص ۶٢)
(سایت ویکی پدیا)
[2] کپلر (Johannes Kepler ۱۵۷۱-۱۶۳۰) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونهای که در یکی از کتابهای خود اینگونه نوشت: «هندسه دارای دو گنج بسیار با اهمیت میباشد که یکی از آنها قضیه فیثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلایی میباشد. اولین گنج را میتوان به طلا و دومی را به جواهر تشبیه کرد»(همان)
[3] اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کردهاست. مصریان، نیز سالها قبل از میلاد از این نسبت آگاه بودهاند و آن را در ساخت اهرام مصر رعایت کردهاند.(همان)
[4] معمولا در ساخت ال سی دیها، مانیتورها، طراحی خودرو و در جاهایی که با اشکال هندسی در ارتباط هستند در حد امکان از نسبت طلایی استفاده میشود. برای نمونه در پرستشگاه باستانی «پارتنون» (Parthenon) در یونان از نسبت طلایی استفاده شده است.(سایت فرادرس،مقاله نسبت طلایی به زبان ساده)
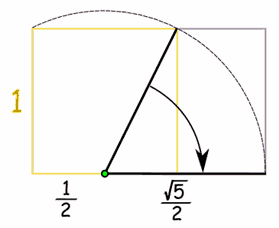
[5] جهت رسم مستطیل طلایی در ابتدا مربعی با اضلاع واحد رسم کنید. سپس مطابق با شکل زیر وسط یکی از اضلاع آن را با استفاده از یک نقطه مشخص کنید و از آن خطی به سمت گوشه سمت راست بکشید. نهایتا با دوران خط مفروض به روی ضلع مربع اولیه، به گوشه مستطیل میرسیم. با رسم مستطیل حاصل از دو نقطه سمت چپ (گوشههای مربع اولیه) و نقطه بدست آمده، مستطیل طلایی بدست میآید.( سایت فرادرس،مقاله نسبت طلایی به زبان ساده)
[6] نسبت طلایی یا عدد فی (ϕ) به انگلیسی:( Golden ratio) در ریاضیات و هنر هنگامی رخ میدهد که نسبت بخش بزرگتر به بخش کوچکتر، برابر با نسبت کل به بخش بزرگتر باشد.تعریف دیگر آن این است که «عددی (ثابت) مثبت است که اگر به آن یک واحد اضافه کنیم، به مربع آن خواهیم رسید (سایت ویکی پدیا)

بدون نظر